ロボットシミュレーション用のルンゲ・クッタ法プログラムの検討（３）１７１７モータのシミュレーション

はじめに

こんにちは、こうへいです。

お正月休みも今日で最後です。だいぶリフレッッシュできたような気がします。今年も仕事に趣味に頑張ろう！

さて、自前のルンゲ・クッタ関数のテストをマイクロマウスでよく使われているFaulhaberの1717T003SRを想定してやってみようと思います。

Faulhaberのモータはマイクロマウスでは最初1724が使われていて、その後で1717が使われ始めたように記憶があります。2000年代のはじめには既にどちらかは使われ始めていたので１５年から２０年ぐらいの長い期間に渡ってクラシックマウスのモータとして君臨してきました。

ハーフが登場してからは、小型電動プレーン用のコアレスモータが主流になり、モータメーカがどこかわからないモータが使われ始めクラシックのモータも変わりつつあるのかなと思いまうす。「中国の通販サイトで安く売られているモータを沢山買って具合の良いものを選ぶ」と言う北陸同好会でのあささんの御講演を聞いて、更にその思いを強くした次第です。あささんのブログにも紹介されていますので引用します。

ブログ更新しました
2019年クラシックマウス華金(HuaJin)についてhttps://t.co/fxMhcmuieA
— あさ🐾 (@Haido_Ele) December 20, 2019

DCモータの数学モデル

f:id:kouhei_ito:20200105205719j:plain — DCモータのモデル

DCモータの数学モデルについて復習してみようと思います。

まずは電流についての回路の方程式

${\displaystyle L \frac{d i}{d t} + R i +K \omega = e }$

つづいて回転に関する運動方程式

${\displaystyle J \frac{d \omega}{d t} + D \omega +T_L = K i }$

各変数は以下の通りです

${i}$ : 電流(A)
${e}$ : 入力電圧 (V)
${\omega}$ : 軸の角速度（rad/s）
${T_L}$ : 負荷トルク（Nm）

各パラメータは以下の通りです　

${L}$ : インダクタンス(H)
${R}$ : 巻線抵抗(Ω)
${K}$ : 逆起電力係数（Vs/rad）、トルク定数（N/A）（同じ値）
${D}$ : 動粘性係数（Nms/rad）
${J}$ : 慣性モーメント（Kg m²）

Faulhaberのデータシートを見ながら各パラメータを調べると

${L}$ : 17 （μH）
${R}$ : 1.07(Ω)
${K}$ : 1.98（mVs/rad）（mN/A）（同じ値）
$D$ : 記載なし
${J}$ : 0.59 (g cm²) 0.59x10^-7 (kg m²)
$\tau_m$ : 機械的時定数 16 (ms)

動粘性係数はモータのデータシートには記載がないのが普通のようです。判らない場合でも他のパラメータで推定できるので、後でそこから推定してみたいと思います。

ルンゲ・クッタ法にかけるのにモータの数学モデルの式を「導関数＝」の形に整理しておきます。

${\displaystyle \frac{d i}{d t}=\frac{e - R i - K \omega}{L} }$

${\displaystyle \frac{d \omega}{d t}= \frac{K i - D \omega -T_L}{J} }$

自前ルンゲ・クッタソルバーrk4に渡すために、それぞれをPythonの関数として書き下すと以下のようになります。　

def idot(t, i, omega, e):
    R=1.07
    K=1.98e-3
    L=17e-5
    return (e - R*i -K*omega)/L 

def omegadot(t, omega, i , T_L):
    K=1.98e-3
    D=0 #現時点で不明なので後で入れる
    J=0.59e-7
    return (K*i - D*omega - T_L)/J

パラメータを関数内に直接書いているところは検討したいところです。 DCモータclassを作って管理するのが、すっきりするかもしれません。

これで、ルンゲ・クッタ法でモータのシミュレーションする準備は整いました。

DCモータの伝達関数

ルンゲ・クッタ法でシミュレーションするだけであれば準備は終わっているのですが DCモータの伝達関数を調べておこうと思います。

DCモータの数学モデルをラプラス変換してみます。

電流の方程式はラプラス変換すると

${\displaystyle L s i(s) + R i(s) +K \omega(s) = e(s) }$

となり、整理すると

${\displaystyle i(s) = \frac{1}{L s + R} e(s) -\frac{K}{Ls+R} \omega(s) }$

同様に回転の方程式をラプラス変換し整理すると

${\displaystyle \omega(s) = \frac{K}{J s + D } i(s) - \frac{1}{J s + D }T_L(s) }$

上記の電流の式を回転の式に代入します

${\displaystyle \omega(s) = \frac{K}{J s + D } \left( \frac{1}{L s + R} e(s) -\frac{K}{Ls+R} \omega(s) \right) - \frac{1}{J s + D }T_L(s) }$

整理すると

${\displaystyle \omega(s) =\frac{K}{JL s^2 + (DL+JR)s + DR+K^2} e(s) - \frac{LS+R}{JL s^2 + (DL+JR)s + DR+K^2} T_L(s) }$

今回は無負荷でのシミュレーションをしたいと思いますので、２項目は無視します。

すると、電圧 $e$ から角速度 $\omega$ までの伝達関数は、１項目の $e$ にかけられている有利関数部分となります。

動粘性係数

実は動粘性係数Dが求まっていませんでした。モータのデータシートには無負荷回転数が示されているので、最終値の定理を用いてDを求めようと思います。

上式に最終値の定理を適用すると

${\displaystyle \omega(\infty) =\lim_{s \to 0} s \frac{K}{JL s^2 + (DL+JR)s + DR+K^2} \frac{3}{s}=\frac{3K}{DR+K^2} }$

無負荷回転数が14000rpmとある、これは1466rad/sなので上式の値がこの値になるためのDを計算すると

D=1.226e-7

となりました。

機械的時定数と電気的時定数

以上でモータの伝達関数が２次振動系であることがわかりました。伝達関数の分母＝０の式を特性方程式と呼びますが、特性方程式の根を制御工学では極と呼びます。モータも普通二つの極があります。

極の絶対値の逆数が時定数になります。 DCモータには、これらの極または時定数で収束の速さが違う二つのモードがあることになります。比較的早く収束するモードの時定数を電気的時定数、遅い方を機械的時定数と呼びます。機械的時定数の方が電気的時定数にくらべてかなり大きいので、電気的時定数に代表されるモードを無視してモータの速度に関する伝達関数を１次遅れとして扱っても良い場合があります。

ただし、電流連続モードのPWM制御を実現しようと思う場合には、電気的時定数を気にしなければなりません。

当ブログでは後日、電流制御のシミュレーションもしてみようと思います。

それぞれの時定数を計算してみたところ

機械的時定数：15.57ms

電気的時定数：15.9 μs

データシートには機械的時定数は15msと書いてあるので、大体良いのではないでしょうか。

データシートの数値は機械的時定数と無負荷回転数に切りの良い数字がでていて実際は若干違うかもと思うのと、モデル化できていない部分が誤差の要因だと思います。上記で無負荷回転数を用いてDを計算していますが、機械的時定数から求める方法もあるので、そうするとシミュレーションしたときに定常状態の回転数がデータシートの値からずれます。

サンプルコードと計算結果

以下に1717シミュレーションのサンプルコードを掲載します。

github.com

計算結果

入力として3Vを加えた時のステップ応答の計算結果を示します。おおよそ時定数が15ms程度、定常速度が1466rad/sのような応答がえられました。

f:id:kouhei_ito:20200106090007p:plain — 1717T003SRモータのステップ応答

前回作成した２次振動系のステップ応答を計算する関数を使って解析解に対しての計算をした結果と比較します。

f:id:kouhei_ito:20200106162558p:plain — 数値計算と解析解との比較

図を見る限り良いようです。

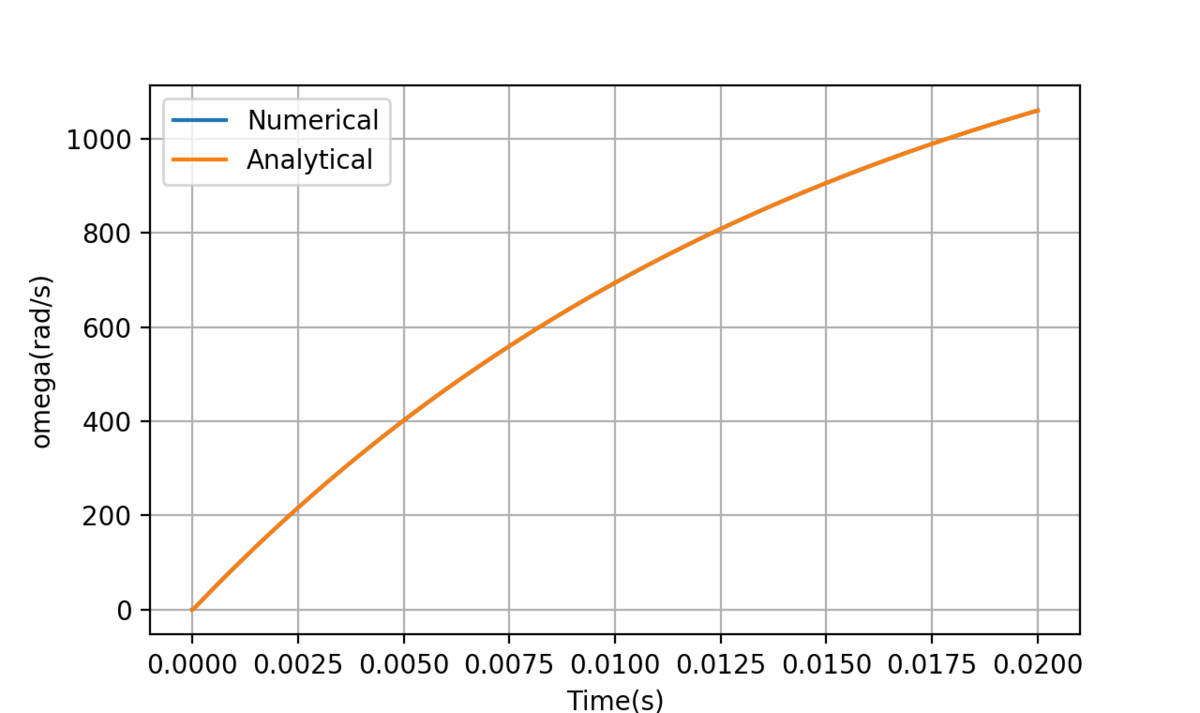
解析解との比較が中途半端な時間で止まっていますが、これは２次振動系のステップ応答関数の中の指数関数がオーバーフロー（無限大に発散）してしまったせいです。コンピュータでの計算においては避けて通れない問題に早くもぶつかった感じです。これについてはまたブログで取り上げたいですね。

おわりに

自前のルンゲ・クッタ関数を使ってモータのシミュレーションをしてみました。マイクロマウスを前提にしても計算の中には二つ以上のモータの計算を別々にしなければなりません。現時点の構成では同じ種類のモータであっても複数の計算をするコードはあまりすっきりと書けないと考えられますので今後はクラスを使ったバージョンも検討してみようかなと思います。

とちゅうで、指数関数がオーバーフローする問題が出ました。小ネタとして以後取り扱いたいと思います。また、次回以降、コードを改良しながらフィードバック制御のシミュレーションなどをしていきたいです。