はじめに
前回、地磁気センサの校正のために楕円体の方程式についてお話ししましたが、今回は 地磁気センサからのデータを集めて、楕円体のパラメータを最小二乗法で推定してみます。
楕円体の方程式
楕円体の方程式は以下の形をしています。
両辺をで割ることでパラメータを一つ減らすことができます。その際も、他のパラメータは元の記号と同じものを使用するとすると、
以下の様に書き換えられます。
最小二乗法
楕円体の方程式の左辺をとします。
地磁気センサから得られた一組のデータをとします。この点が楕円体の面上に位置しているとすると、
が成立します。
しかし、取得されたセンサーデータは楕円体の近傍に位置していても、完全に楕円体面上にはほとんどの点が存在していないため、
は成立しません。
ここで、全ての取得データに対して最も近い楕円体のパラメータ(〜
)を求めたいと思います。
そこで、最も近い楕円体の定義を以下の評価関数を最も小さいものにするパラメータをもつ楕円体とします。
これを解いて、パラメータを求める手法がお馴染みの最小二乗法です。
正規方程式を求める
最小値問題は各パラメータでの偏導関数が0となるパラメータを求める問題になります。
評価関数を9個のパラメータで編微分してできる9元連立方程式を正規方程式と呼びます。
各パラメータに関する偏微分を求めていく作業は単純作業で間違いやすく、退屈なものですが、淡々とこなしていきます。
上記はパラメータ分だけを示したものです。これを全てのパラメータで行います。
各パラメータで偏微分した方程式に現れる係数だけをマトリックス状にして以下に示します。
なお、以下は
が省略されています。1行目と1列目は検算をして間違いを防ぐことができる様に添えています。
黄色とオレンジ色の部分が係数マトリックスです。
パラメータが要素となっている以下のベクトルを定義します。
上記のマトリックスの黄色の部分で構成される行列をとし
オレンジ色の部分で構成されるベクトルを
とすると、
以下のような行列ベクトルで表した連立方程式となります。
これは未知数が9個の9元連立方程式となります。これを正規方程式と呼びます。
解は逆行列を用いて以下になります。
実際のデータによるフィッティング
以前9DOFセンサによるデータ取得について触れました。
センサを色々な方向に回しながらデータをとり、その結果を散布図として図示したものが次の図になります。
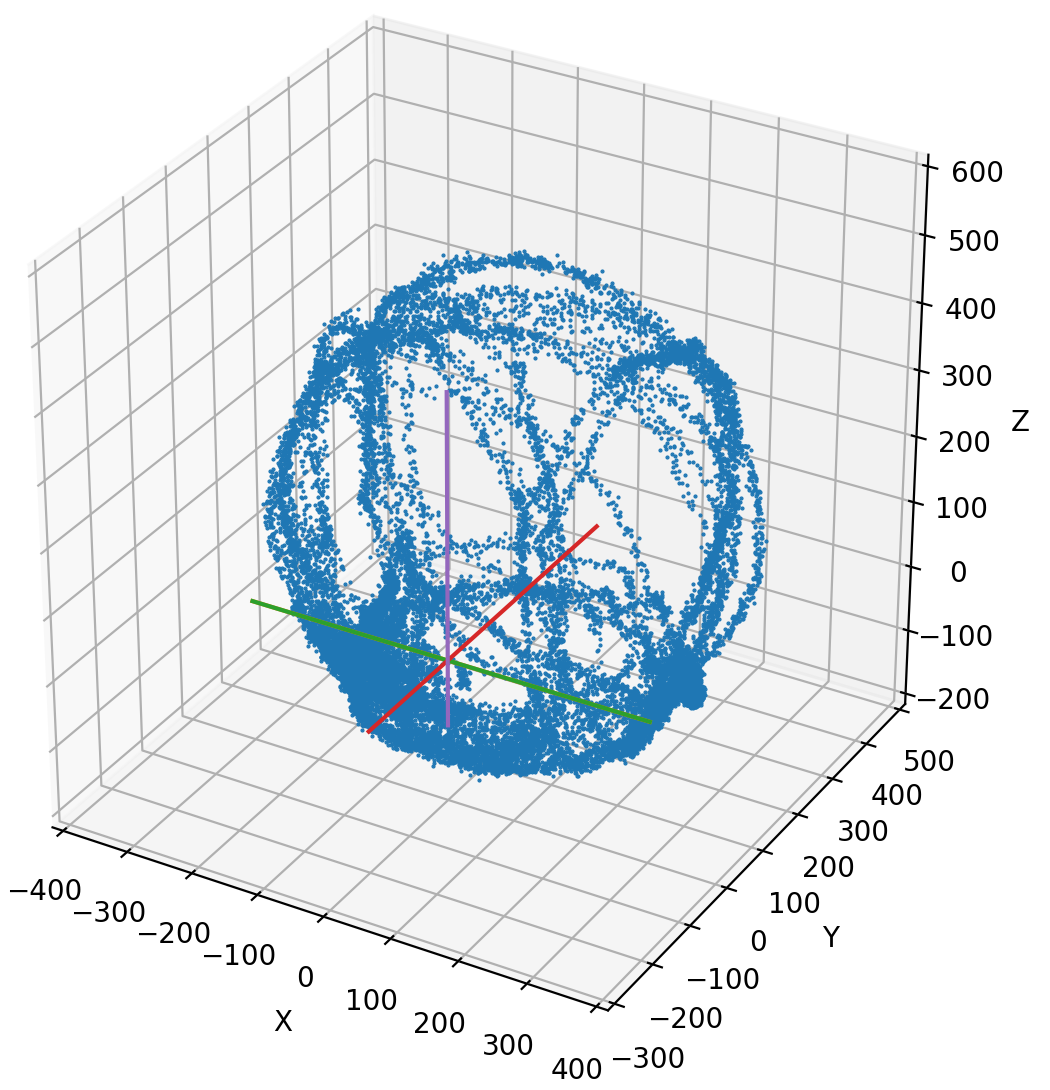
図の様に、地磁気データはオフセットしていることが、明確にわかります。
楕円体かどうか、あるいは、傾いているかどうかはこの図からははっきりとは読み取れません。
このデータに上記の最小二乗法を当てはめて、楕円体方程式のパラメータを求めます。
楕円体のパラメータ抽出と回転・並行移動のコード
実際の計算をpythonを用いて行いました。 実装に当たっては、2次のパラメータ行列の固有ベクトルをどの順に並べるかを考慮する必要があります。
参考までに、以下にコードを示します。 jupyter環境で実行しています。jupyterでなければ最初の%のついている行を削除してください。
%matplotlib widget import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D #data00csv.txtの最後の3列がmG(ミリガウス)単位の地磁気データx、y、zとなっている data=np.loadtxt('data00csv.txt', delimiter=',') #地磁気データ抽出 magx=-data[:,6] magy=data[:,7] magz=-data[:,8] #最小二乗法 #正規方程式の作成 #1 x2 _x4=sum(magx**4) _x2y2 =sum(magx**2*magy**2) _x2z2 =sum(magx**2*magz**2) _2x3y =sum(2*magx**3*magy) _2x2yz=sum(2*magx**2*magy*magz) _2x3z =sum(2*magx**3*magz) _x3 =sum(magx**3) _x2y =sum(magx**2*magy) _x2z =sum(magx**2*magz) #2 y2 _y4 =sum(magy**4) _y2z2 =sum(magy**2*magz**2) _2xy3 =sum(2*magx*magy**3) _2y3z=sum(2*magy**3*magz) _2xy2z=sum(2*magx*magy**2*magz) _xy2 =sum(magx*magy**2) _y3 =sum(magy**3) _y2z =sum(magy**2*magz) #3 z2 _z4 =sum(magz**4) _2xyz2=sum(2*magx*magy*magz**2) _2yz3=sum(2*magy*magz**3) _2xz3 =sum(2*magx*magz**3) _xz2 =sum(magx*magz**2) _yz2 =sum(magy*magz**2) _z3 =sum(magz**3) #4 xy _2x2y2=sum(2*magx**2*magy**2) _2xy2z=sum(2*magx*magy**2*magz) _2x2yz=sum(2*magx**2*magy*magz) _x2y =sum(magx**2*magy) _xy2 =sum(magx*magy**2) _xyz =sum(magx*magy*magz) #5 yz _2y2z2=sum(2*magy**2*magz**2) _2xyz2=sum(2*magx*magy*magz**2) _xyz =sum(magx*magy*magz) _y2z =sum(magy**2*magz) _yz2 =sum(magy*magz**2) #6 xz _2x2z2=sum(2*magx**2*magz**2) _x2z =sum(magx**2*magz) _xyz =sum(magx*magy*magz) _xz2 =sum(magx*magz**2) #7 x _x2 =sum(magx**2) _xy =sum(magx*magy) _xz =sum(magx*magz) #8 y _y2 =sum(magy**2) _yz =sum(magy*magz) #9 z _z2 =sum(magz**2) #b _x=sum(magx) _y=sum(magy) _z=sum(magz) #正規行列 M=np.matrix([[ _x4, _x2y2, _x2z2, _2x3y, _2x2yz, _2x3z, _x3, _x2y, _x2z], [ _x2y2, _y4, _y2z2, _2xy3, _2y3z, _2xy2z, _xy2, _y3, _y2z], [ _x2z2, _y2z2, _z4, _2xyz2, _2yz3, _2xz3, _xz2, _yz2, _z3], [ _2x3y/2, _2xy3/2, _2xyz2/2, _2x2y2, _2xy2z, _2x2yz, _x2y, _xy2, _xyz], [_2x2yz/2, _2y3z/2, _2yz3/2, _2xy2z/2, _2y2z2, _2xyz2, _xyz, _y2z, _yz2], [ _2x3z/2, _2xy2z/2, _2xz3/2, _2x2yz/2, _2xyz2/2, _2x2z2, _x2z, _xyz, _xz2], [ _x3, _xy2, _xz2, _x2y, _xyz, _x2z, _x2, _xy, _xz], [ _x2y, _y3, _yz2, _xy2, _y2z, _xyz, _xy, _y2, _yz], [ _x2z, _y2z, _z3, _xyz, _yz2, _xz2, _xz, _yz, _z2] ]) b=np.matrix([_x2, _y2, _z2, _xy, _yz, _xz, _x, _y, _z]).T #楕円体パラメータの算出 x=np.linalg.inv(M)*(-b) print('楕円体パラメータ') print(x) a11=x[0,0] a22=x[1,0] a33=x[2,0] a12=x[3,0] a23=x[4,0] a13=x[5,0] b1 =x[6,0] b2 =x[7,0] b3 =x[8,0] #楕円体2次項パラメータ行列 A=np.matrix([[a11,a12,a13],[a12,a22,a23],[a13,a23,a33]]) #2次項パラメータ行列の固有値と固有ベクトルを求める lbda,v=np.linalg.eig(A) print('固有値・固有ベクトル') print(lbda) print(v) #回転・並行移動 #固有値と基底ベクトル(固有ベクトル)の並べ替え vt=v.T vx=vt[1].T vy=vt[2].T vz=vt[0].T lbdx=lbda[1] lbdy=lbda[2] lbdz=lbda[0] #1次項のパラメータベクトル B=np.matrix([b1,b2,b3]) #対角化行列(回転行列) P=np.hstack([vx,vy,vz]) print('回転行列') print(P.T) #楕円体の中心座標算出 x0=(-B*vx/2/lbdx)[0,0] y0=(-B*vy/2/lbdy)[0,0] z0=(-B*vz/2/lbdz)[0,0] print('中心座標') print(x0,y0,z0) #球に変換 W=(B*vx)[0,0]**2/4/lbdx + (B*vy)[0,0]**2/4/lbdy + (B*vz)[0,0]**2/4/lbdz -1 print('W') print(W) sx=np.sqrt(lbdx/W) sy=np.sqrt(lbdy/W) sz=np.sqrt(lbdz/W) smax=max(sx,sy,sz) sx=sx/smax sy=sy/smax sz=sz/smax print('拡大係数') print(sx, sy, sz) #移動計算のためデータ整形 mag2=np.vstack([magx,magy,magz]) #回転 mag2=P.T*mag2 #並行移動 magx2=np.array(mag2)[0]-x0 magy2=np.array(mag2)[1]-y0 magz2=np.array(mag2)[2]-z0 #拡大縮小 magx2=sx*magx2 magy2=sy*magy2 magz2=sz*magz2 #データのプロット # グラフの枠を作成 fig = plt.figure(figsize=(7,7)) ax = fig.add_subplot(111, projection='3d') # X,Y,Z軸にラベルを設定 ax.set_xlabel("X") ax.set_ylabel("Y") ax.set_zlabel("Z") ax.set_xlim([-500,500]) ax.set_ylim([-400,600]) ax.set_zlim([-600,400]) ax.set_box_aspect((1,1,1)) # 生データ描画 ax.plot(magx,magy,magz,marker=".",ms=1, linestyle='None') #回転・平行移動後の描画 ax.plot(magx2,magy2,magz2,marker=".",ms=1, linestyle='None') #規定ベクトルの描画 ax.plot([0+x0,v[0,0]*200+x0],[0+y0,v[1,0]*200+y0],[0+z0,v[2,0]*200+z0], marker='*') ax.plot([0+x0,v[0,1]*200+x0],[0+y0,v[1,1]*200+y0],[0+z0,v[2,1]*200+z0], marker='*') ax.plot([0+x0,v[0,2]*200+x0],[0+y0,v[1,2]*200+y0],[0+z0,v[2,2]*200+z0], marker='*') #xyz軸描画 ax.plot([-500,500],[0,0],[0,0]) ax.plot([0,0],[-400,600],[0,0]) ax.plot([0,0],[0,0],[-400,600]) # グラフ表示 plt.show()
githubにも地磁気データとともに置いておきます。
おわりに
下図の様に、得られた地磁気データから楕円体方程式のパラメータを推定し、 前回お話しした楕円体の方程式の知識から、回転と平行移動を施してみました。
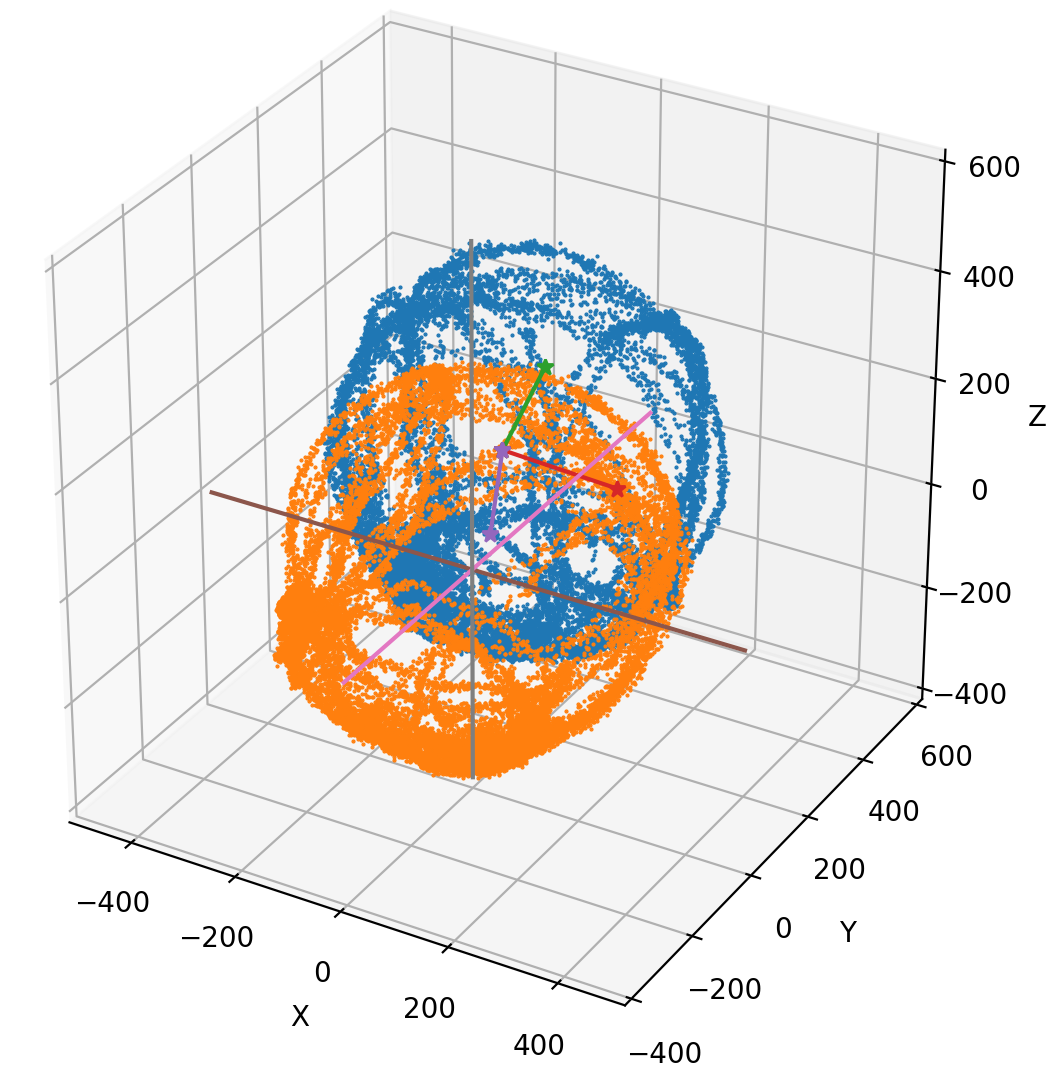
この様に、得られたデータからマルチコプタで地磁気センサを活用するための校正作業を進めていきます。 以上の他は、前回の記事にもありますがx、y、z方向の半径に当たる量を求め、楕円を引っ張ったり縮めたりして 球体に補正すると校正終了となります。
最小二乗法の偏微分を間違いなく、そしてコーディングの際にそれを更に間違いなく打ち込むのに苦労しました。 何回か間違いを修正して、やっと納得いく計算結果が得られました。 同じ様なことをされる際の参考になればと思います。
それでは。また!