マクローリン展開の打切り誤差をCOS関数で検証

f:id:kouhei_ito:20200510230524p:plain

はじめに

こんにちは、こうへいです

マイクロマウスのようなロボットの走行軌跡の計算には三角関数を含んだ積分をしなければならないんですが、その場合、解析的に答えを出せないことの方が多く、数値積分に頼らなけらばなりません。

そこで、数値積分ではなく三角関数をマクローリン展開した多項式を適当な次数で打ち切ってその式を積分したらうまくいくかも！

と考えてみました。ところがマイクロマウスのスラローム走行の検討で、同じことを鯉住さんが既に検討しているのを見つけてしまいみなさん似たような事を考えられていると感心しました。

tenpura.sugo-roku.com

自分もマウスのプログラムを少し書いていたので、新しいものには新しい試みを載せてみたく思いました。

まずは、マクローリン展開の近似精度を計算して可視化して遊んでみようと思った次第です。はやく諸先輩方に追いつきたいものです。

前回、jupyter labの環境紹介したのでそれを使った計算にもなります。

マクローリン展開

関数の級数展開

何回でも微分可能な関数は次の式で示されるマクローリン展開（テイラー展開）によって、近似式が得れれます。

$f(x)={\displaystyle\sum_{k=0}^{\infty}}f^{(k)}(0)\dfrac{x^k}{k!}\\=f(0)+f'(0)x+\dfrac{f”(0)}{2!}x^2+\dfrac{f^{(3)}(0)}{3!}x^3\cdots$

sinとcosのマクローリン展開

三角関数については以下のように展開されます。

$\sin x={\displaystyle\sum_{k=0}^{\infty}}(-1)^k\dfrac{x^{2k+1}}{(2k+1)!}=x-\dfrac{x^3}{6}+\cdots\\ \cos x={\displaystyle\sum_{k=0}^{\infty}}(-1)^k\dfrac{x^{2k}}{(2k)!}=1-\dfrac{x^2}{2}+\cdots$

Pyrhonで計算してみる

コード

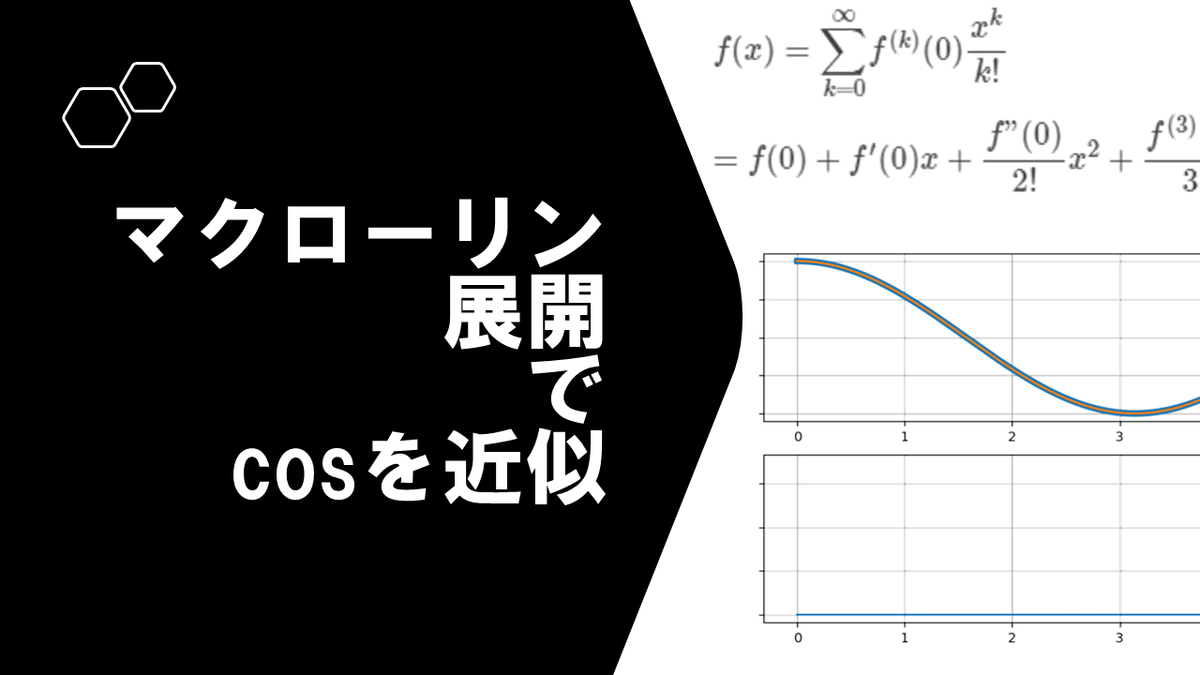
Jupyter lab用に書いたcos関数のマクローリン展開近似を計算して、 numpyのcos関数の結果を比較して、誤差も合わせて示すプログラムを以下にしまします。

%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt

#階乗関数
def factrial(x):
    if x>1:
        return x*factrial(x-1)
    else:
        return 1

#cos関数のマクローリン展開
def mycos(x,n):
    s=0
    for k in range(n):
        s=s+(-1)**k*x**(2*k)/factrial(2*k)
    return s

x=np.linspace(0, 2*np.pi, 200)
y=np.cos(x)
my=mycos(x, 5)
plt.figure(figsize=(10, 5))
plt.subplot(211)
plt.plot(x, y, lw=5)
plt.plot(x, my)
plt.ylabel('cos(x)')
plt.grid()
plt.subplot(212)
plt.plot(x, y-my)
plt.ylabel('Error')
plt.grid()
plt.show()

階乗計算関数とcos関数のマクローリン展開のmycos関数を自作しました。

mycos関数の第2引数が展開次数です。

計算結果

マクローリン展開は原点付近の近似式なので、原点から離れれば誤差が増えるはずです。定義域を０から２πとして以下の計算をしてみました。

5次までの級数展開

f:id:kouhei_ito:20200510220534p:plain — 5次までの級数展開

10次までの級数展開

f:id:kouhei_ito:20200510220723p:plain — 10次までの級数展開

２πまでの範囲ならば１０次まで展開すると、かなりcos関数に近いことがわかりました。

ちなみに１０次の項の分母の階乗は20!＝2432902008176640000となりとてつもなく大きくなり、マイコン等で計算するのがギリギリです。

三角関数はπ／４まででOK

三角関数はπ／４まで計算すると、あとは線対称な形状をしているので、そこまでの値があればすべての定義域での値が得られる。すると、以下のように5次ぐらいの近似で使えそうです。実用上はもう少し下げても行けそうな気がします。

f:id:kouhei_ito:20200510222108p:plain — π／４までを5次で級数展開した結果

最後に１０次まで重ねてみた

f:id:kouhei_ito:20200511010040p:plain これを見ると、π／４までなら4次でも良さそうです。

上のグラフのコード

%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt

def factrial(x):
    if x>1:
        return x*factrial(x-1)
    else:
        return 1

def mycos(x,n):
    s=0
    for k in range(n):
        s=s+(-1)**k*x**(2*k)/factrial(2*k)
    return s

plt.figure(figsize=(8, 5))
x=np.linspace(0, 2*np.pi, 200)
y=np.cos(x)
plt.plot(x, y, lw=3, label='cos(x)')
for n in range(10):
    my=mycos(x, n+1)
    plt.plot(x, my, label='n={}'.format(n+1))
plt.xlim(0, 2*np.pi)
plt.ylim(-1.02, 1.02)
plt.ylabel('cos(x)')
plt.legend()
plt.grid()
plt.show()