移動ロボットの壁沿い走行制御について

移動ロボットの壁沿い走行制御についてアイキャッチ

はじめに

マイクロマウスの様な移動ロボットを壁に沿って走らせたいと言う場面は、教育用のデモ走行やその他の簡単なアプリケーションでは多く見かけられると思います。

何かの軌跡に沿って走らせたいと言うのもさらなる応用として考えられます。

今回は無限に続く壁に沿って移動ロボットを走らせるための誘導制御について考えてみたいと思います。

はじめに
壁沿い走行のモデル
誤差の微分をフィードバックする
- システムの極について
  - 線形シミュレーションと非線形シミュレーションの比較
- センサ情報から位置の推定手法による違い
おわりに
参考文献
付録
- 誤差に比例して角速度指令
- 誤差とその微分の両方に比例して角速度指令とする方法

壁沿い走行のモデル

諸々の設定

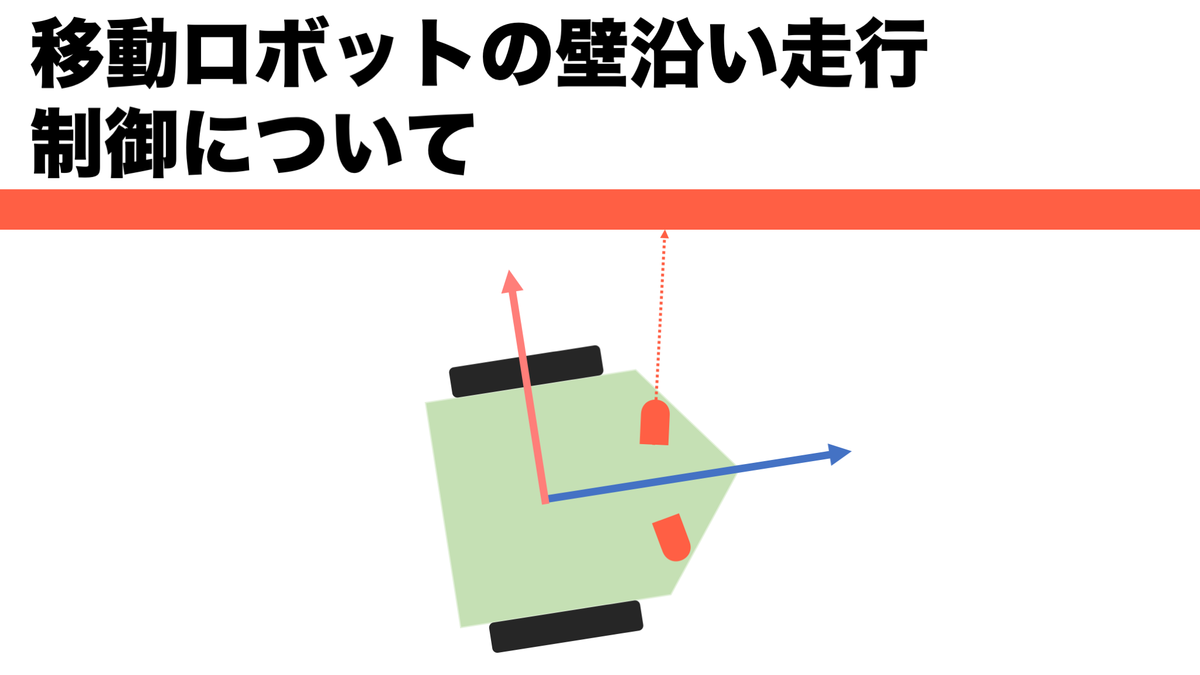
ロボットは片側に壁があってその壁に沿って壁との距離を検知できるセンサを用いて壁沿い走行を実現するとします。

ロボットの重心の座標を( $x_m$ , $y_m$ )

ロボットの傾きを $\psi$

センサのロボット重心からの位置を( $x_{ms}$ , $y_{ms}$ )

センサのロボットに対する取り付け角度を $\alpha_s$

マイクロマウスで言えば迷路の様な走行する場をグローバル座標空間としてグローバル座標空間において、x軸に平行に壁があるとします。

壁の座標は $y=d$

ロボットは壁に沿ってx軸の正方向に向かって走行します。うまく走行すればx軸に平行に移動することになります。

ロボットの走行速度は一定として $V$ とします。

グローバル座標空間におけるセンサの位置

壁沿い走行を分析するためにセンサの位置の変化を表す数学モデルを導いてみます。

走行中ロボットがx軸に対して傾くとするとその傾きと、ロボットの位置を加味してセンサの位置を算出すると次のようになります。

$\begin{eqnarray} x_s = x_{ms} \cos \psi - y_{ms} \sin \psi + x_m\\ y_s = x_{ms} \sin \psi + y_{ms} \cos \psi + y_m\\ \end{eqnarray}$

今回の検討ではロボットは滑らないと考えます。ロボットの速度を $V$ とし、ロボットの向いている方向 $\psi$ は速度の方向と一致しますので、x軸方向とy軸方向の速度成分はそれぞれ次の様になります。

$\begin{eqnarray} v_x = V \cos \psi \\ v_y = V \sin \psi \\ \end{eqnarray}$

ロボットの位置は速度の積分なので

$\begin{eqnarray} x_m = V \int \cos \psi dt\\ y_m = V \int\sin \psi dt \\ \end{eqnarray}$

したがって、センサのグローバル座標上での位置については以下のようになります。

$\begin{eqnarray} x_s = x_{ms} \cos \psi - y_{ms} \sin \psi + V \int \cos \psi dt\\ y_s = x_{ms} \sin \psi + y_{ms} \cos \psi + V \int \sin \psi dt\\ \end{eqnarray}$

センサはロボットに対して $\alpha_s$ で取り付けられており、走行中のロボットの傾きが $\psi$ としますとセンサはグローバル座標に対して、 $\alpha_s+\psi$ 傾いていることになります。

そうするとセンサが検知する壁までの距離 $R$ とセンサの壁からの距離 $d-y_s$ は角 $(\alpha_s+\psi)$ に対して直角三角形の斜辺と対辺の関係になります。

センサから得られる距離情報は $R$ ですが、壁沿い走行を目的とする際に「壁から一定の距離を保つ」という制御目標に対しては傾いているセンサからの情報 $R$ を一定に保つと言うよりも $d-y_s$ を一定に保つあるいは $y_s$ をある値にすると行った方が見通しが良い様な気がします。

仮にジャイロを搭載したロボットであれば角速度から $\psi$ を推定することも容易になるので

$\begin{eqnarray} d-y_s= R sin (\alpha_s + \psi) \end{eqnarray}$

の様にセンサから得られた $R$ と推定したセンサの傾きから壁とセンサの位置関係を推定できます。ちなみに、 $\alpha_s=90^o$ の時はセンサの情報がロボットの壁からの距離を表しますので両者は一致します。

さらに $y_s$ について解けばセンサ情報と推定した角度と既知情報から $y_s$ を以下の様に推定できます。

$\begin{eqnarray} y_s = d - R sin (\alpha_s + \psi) \end{eqnarray}$

今回はこの $y_s$ を一定にする制御をしてみようと思います。これはロボットの中のセンサの位置が $y_{ms}$ なのでそこから重心位置の推定も容易にできるのでロボットの重心位置を制御していることと本質的に違いはありません。

これは直感的にわかりやすいと言うこともありますが、上で示した $y_s$ の式が容易に線形化できて、線形解析でゲインの決定なども検討できると言うのが理由です。

通常まず試すことは $R$ をフィードバックして距離を一定にする試みですが、本記事ではのちほどその方法についても比較してみます。

線形化

$y_s$ についての式を再掲します。

$\begin{eqnarray} y_s = x_{ms} \sin \psi + y_{ms} \cos \psi + V \int \sin \psi dt\\ \end{eqnarray}$

$\psi$ があまり大きくならないとする前提をおきます。

そうすると、三角比の部分を近似して $\sin \psi$ は $\psi$ へ、 $\cos \psi$ は１となり、以下の様に書き直すことができます。

$\begin{eqnarray} y_s = x_{ms} \psi + y_{ms} + V \int \psi dt\\ \end{eqnarray}$

積分方程式もあまり馴染みがないので、両辺を微分します。

$\begin{eqnarray} \dot{y}_s = x_{ms} \dot{\psi} + V \psi\\ \end{eqnarray}$

以上で線形化された、壁とセンサの位置関係に関するモデルが得られました。

誘導則

ロボットを壁沿いに誘導するための誘導則を考えましょう。

簡単な方法に、目標値 ${y_s}_{ref}$ と $y_s$ との誤差にゲイン $K$ をかけたものを、ロボットの角速度指令とする方法です。

ロボットの角速度は $\dot{\psi}$ なので、既にモデルの中に現れています。

実際のロボットは指令角速度に対してダイナミクスを持って実際に角速度が現れますが、今回の検討では無視します。無視した影響は角速度の応答が遅い場合に振動的になって現れたり制御性能の低下で現れますが、そこはまたの話題にできたらと思います。

誘導則を式に表しますと

$\begin{eqnarray} \dot{\psi}=K ({y_s}_{ref} - y_s) \end{eqnarray}$

フィードバックシステムの状態方程式

既出の位置線形モデルを再掲します

$\begin{eqnarray} \dot{y}_s = x_{ms} \dot{\psi} + V \psi\\ \end{eqnarray}$

上式に誘導則を代入すると

$\begin{eqnarray} \dot{y}_s = x_{ms} K ({y_s}_{ref} - y_s) + V \psi\\ \end{eqnarray}$

展開すると

$\begin{eqnarray} \dot{y}_s = - x_{ms} K y_s + V \psi + x_{ms} K {y_s}_{ref} \\ \end{eqnarray}$

誘導則についても展開すると

$\begin{eqnarray} \dot{\psi}=- K y_s + K {y_s}_{ref} \end{eqnarray}$

上記２式を状態方程式としてみると、行列形式で以下の様に示すことが可能です。

$\displaystyle{ \begin{bmatrix} \dot{x_s} \\ \dot{\psi} \end{bmatrix} = \begin{bmatrix} - x_{ms} K & V\\ -K & 0 \end{bmatrix} \begin{bmatrix} x_s \\ \psi \end{bmatrix} + \begin{bmatrix} x_{ms} K \\ K \end{bmatrix} {y_s}_{ref} }$

(※上記には行列の数式が記述されていますがiPhoneのはてなブログアプリでは正しく表示されません．)

誘導制御の目標

これから誘導ゲインを決めていきますが、誘導制御の目標をざっくりと定めておきたいと思います。

オーバーシュートしない
0.1秒程度で収束する

以上を目標としてゲインを定めていきたいと思います。

誘導ゲインの決定

左辺の最初の行列をシステム行列と呼びますが、システム行列の固有値の実部が全て正であればシステムは安定です。

ここで、行列 $A$ の固有値 $\lambda$ は以下の行列式で表される方程式の解となります。

$\begin{eqnarray} \left|A-\lambda I \right| = 0\\ \end{eqnarray}$

前述のシステム行列は２x２なのでそれほど計算も大変ではなく固有値を求める方程式は以下の２次方程式となります。

$\begin{eqnarray} \lambda^2 + x_{ms} K \lambda + KV =0\\ \end{eqnarray}$

従って、解の公式に当てはめると

$\begin{eqnarray} \lambda=\frac{-x_{ms}K \pm \sqrt{x_{ms}^2 K^2 - 4KV}}{2} \end{eqnarray}$

判別式部分からゲイン $K$ の値の範囲で次の様に分類できます。

固有値が異なる二つの実数

$\begin{eqnarray} K>\frac{4V}{x_{ms}^2} \end{eqnarray}$

解の公式による $\lambda$ から明らかですが、二つの実数解はいかなる $K$ に対しても負の数となり、システムは安定です。

固有値が重解

$\begin{eqnarray} K=\frac{4V}{x_{ms}^2} \end{eqnarray}$

固有値が共役複素解

$\begin{eqnarray} K<\frac{4V}{x_{ms}^2} \end{eqnarray}$

共役複素解になった場合は挙動が振動的になるので避けたいところです。

誘導ゲイン $K$ については固有値が重解になる値を境に挙動が変わることになります。ゲイン決定にあたってはその値を目安に試行錯誤をすることがお勧めです。

数値計算

数値計算をして確認をしてみます。

計算におけるパラメータは以下の様にしてみました。

名称	記号	値	単位
速度	V	0.8	m/s
センサ位置	$x_{ms}$	0.04	m
センサ初期位置		0.03	m
目標位置	${y_s}_{ref}$	0.04	m

この設定の場合、重解になる誘導ゲイン $K$ の値は2000ですので、この値でシミュレーションしてみます。

結果は以下の様になります。

PsiDotは $\dot{\psi}$ を表していますが、実際のロボットでは限界がありますので、仮に７２０deg/sぐらいが限界だとすると、上の結果は大きすぎるので、ゲインを小さくしなければなりません。

初期位置誤差は０．０１mなのでその誤差から７２０deg/sの角速度以内に抑える誘導ゲイン $K$ の値はおおよそ１２５７となります。この値でシミュレーションをすると。

多少立ち上がりが遅くなりましたが、角速度は抑えることができました。誘導ゲインが重解となる２０００を下回っているので、若干振動的な応答となっています。

角速度の物理的限界を考慮した最大の誘導ゲインが１２５６となるのでこれ以下にして更に振動的な挙動にする必要性はないので、このパラメータではこの値が最適な誘導ゲインとなります。

少しオーバシュートしていますが、これを改善することは誘導ゲインを調整しただけでは不可能です。

壁誘導システムの伝達関数

壁誘導システムの状態方程式を再掲します。

$\left\{ \begin{eqnarray} \dot{y}_s&=& - x_{ms} K y_s + V \psi + x_{ms} K {y_s}_{ref} \\ \dot{\psi}&=&- K y_s + K {y_s}_{ref} \end{eqnarray} \right.$

伝達関数を求めるためにラプラス変換すると

$\left\{ \begin{eqnarray} s {y}_s&=& - x_{ms} K y_s + V \psi + x_{ms} K {y_s}_{ref} \\ s\psi&=&- K y_s + K {y_s}_{ref} \end{eqnarray} \right.$

整理すると

$\left\{ \begin{eqnarray} {y}_s&=& \frac{V}{s +x_{ms} K } \psi +\frac{ x_{ms} K}{s +x_{ms} K } {y_s}_{ref} \\ \psi&=&-\frac{K}{s} y_s + \frac{K}{s} {y_s}_{ref} \end{eqnarray} \right.$

２式から $\psi$ を消去して、まとめると $y_s$ に関する伝達関数が求まる

$\begin{eqnarray} y_s=\frac{K(x_{ms} s +V)}{s^2 + x_{ms} K s + KV} {y_s}_{ref} \end{eqnarray}$

減衰係数と自然角周波数

分母多項式は２次遅れ系の形をしているので、減衰係数を $\zeta$ 、自然角周波数を $\omega_n$ として

$\begin{eqnarray} y_s=\frac{K(x_{ms} s +V)}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} {y_s}_{ref} \end{eqnarray}$

と書き直すと

$\left\{ \begin{eqnarray} 2\zeta \omega_n = x_{ms} K\\ {\omega_n}^2=KV \end{eqnarray} \right.$

となり、減衰係数や自然角周波数を誘導ゲイン $K$ を用いて表すと以下の様になります。

$\left\{ \begin{eqnarray} \zeta = \frac{x_{ms}}{ 2} \sqrt{\frac{K}{V}}\\ \omega_n=\sqrt{KV} \end{eqnarray} \right.$

本誘導システムは純粋な２次遅れ系ではありませんが、目安として誘導ゲインに対しての減衰係数と自然角周波数の変化を見ておきたいと思います。

数値例については先ほどと同じ例を使いたいと思います。

前の検討でも述べましたが、K=2000で減衰係数が１になるのがわかります。減衰係数については

$0＜\zeta＜1$ ：　不足減衰（Under damping）
$\zeta=1$ ：　臨界減衰（Critical damping）
$\zeta>1$ ：　過減衰（Over damping）

であるので、固有値（極）が重解になるところがちょうど臨界減衰です。両方のグラフを見ると相似になっています。それぞれの値の式はよく見ると $\sqrt{K}$ の定数倍だと言うことがわかり納得できます。

標準の２次遅れ系は次の様な形をしていてステップ応答は１に収束します。

$\begin{eqnarray} y_s=\frac{{\omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} {y_s}_{ref} \end{eqnarray}$

標準の２次遅れ系ならば減衰係数が１の時オーバーシュートせずに収束するはずなのですが、本誘導システムでは減衰係数が１になる誘導ゲイン $K=2000$ において、オーバーシュートの様なものがみられます。

これは何故かと言うことを少し考えてみると、本システムの伝達関数を少し書き換えてみると

$\begin{eqnarray} y_s=\frac{{\omega_n}^2 (\frac{x_{ms}}{V} s +1)}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} {y_s}_{ref} \end{eqnarray}$

これをみると本誘導システムは２次振動系に位相進み要素がかけられています。この位相進み要素がオーバーシュートの部分を生じさせていると考えることができます。

さて、本誘導システムでは、誘導ゲイン $K$ と速度 $V$ は変えられます、ロボットの設計段階ではさらに $x_{ms}$ も変えることができます。これまで見てきた式から、 $K$ を大きくすると自然角周波数も大きくなり即応性が向上し、減衰係数も大きくなるから振動的な挙動が抑えられます。

また速度 $V$ を大きくすると、やはり自然角周波数も大きくなり即応性が向上します。しかし、減衰係数は小さくなるため振動的な傾向が増します。また、速度は狙いたい速度があるため誘導制御のパラメータとして扱うのは不適切な様な気がします。

設計時に決められるセンサの位置 $x_{ms}$ ですが、これを大きくすると減衰係数が大きくなり振動的な挙動を抑えられますが、分母の位相進みの部分は周波数が低いところで位相が進みます。

これらをについてシミュレーションによる確認をしてみたいと思います。

まず速度 $V$ と $x_{ms}$ を上の数値例に固定して $K$ を変えた場合です。

明らかに、誘導ゲインを大きくすると即応性も上がり、オーバーシュートも下がっていくのですが、必要な角速度を抑えることはできません。

そこで、先ほどと同様、妥当な角速度に収まる様にK=1250に設定します。

次に、設計時に決めるセンサーの位置によっての挙動の変化をみてみます。

センサーの位置を前に出せば出すほど減衰性が上がって、望ましい応答に近づくことがわかります。ライントレースロボットのセンサーが前に長く出ているのをみることがありますが、その点と共通の部分であると考えます。

とは言え、センサの位置を前に出すにも限界があると思いますので、制限がある中で最も前に出すのが有効な様です。

さてここまで位置誤差の定数倍をフィードバックする誘導則についてみてきましたが誘導ゲイン $K$ の調整だけではオーバーシュートをなくすためには大きなゲイン設定が必要であり、角速度の限界もあるため不可能であることがわかりました。

また、減衰係数や自然角周波数と言った値もそれぞれ別々に望ましい値には設定できないこともわかりました。

設計時にセンサー位置などをできるだけ前に出すことで減衰性が向上することも理解できました。

誤差の微分をフィードバックする

壁沿い走行を実現するための誘導方法として次に候補としては角速度の目標値を誤差の定数倍＋誤差の微分の定数倍という誘導方法があります。

これはいわゆるPD制御でオーバーシュートの低減や振動的な挙動の改善が見込まれるはずです。

誘導法則も含めたシステムの方程式を以下に記述します。

$\left\{ \begin{eqnarray} \dot{y}_s &=& x_{ms} \dot{\psi} + V \psi\\ e&=&{y_s}_{ref} - y_s\\ \dot{\psi}&=&K_p e + K_d \dot e\\ \end{eqnarray} \right.$

２式目が位置誤差で３式目が誘導則です。誤差の $K_p$ 倍＋誤差の微分の $K_d$ 倍を目標角速度とします。

これらの方程式をまとめて $\dot \psi$ について解くと

$\begin{eqnarray} \dot \psi =\frac{K_p}{1+K_d x_{ms}} e - \frac{K_d}{1+K_d x_{ms}}V\psi \end{eqnarray}$

このように $\dot \psi$ について解いてみると位置の微分をすることなく $\psi$ をフィードバックすることで誘導則を実現することができます。微分を作るのは危険なのでなるべくなら行いたくないので、良い方法だと考えられます。

ただし $\psi$ に関してはジャイロ角速度の積分など、これまたバイアスによるドリフトなどいろいろな問題もありますので、一概に素晴らしいとも言えません。何かしらの方法で $\psi$ を推定する方法を考えるのも面白いかと思います。

この誘導システムの目標値は大きさ $r$ のステップ入力とし、初期位置は０としたときの誘導システムのステップ応答を表す式は以下の様になります。

$\begin{eqnarray} y_s(s) =\frac{ (x_{ms} s + V)(K_d s +K_p) }{ (1+x_{ms}K_d)s^2+(K_dV+K_p x_{ms})s+K_pV} \frac{r}{s} \\ -\frac{ (x_{ms} s + V)}{ (1+x_{ms}K_d)s^2+(K_dV+K_p x_{ms})s+K_pV} r\\ \end{eqnarray}$

初期位置の設定がこれまでの数値例とちがいます。初期位置を考慮して式を立てると更に式が長くなりますが、初期位置を組み入れることは制御系の検討に重要な要素ではないので省略しました。

システムの極について

このシステムの極が２実数解、複素共役解、２重解になるかでシステムの挙動が変化するわけですが分母の２次方程式の判別式は次の様になります。

$\begin{eqnarray} D=(K_d V + K_p x_{ms})^2 -4K_pV \end{eqnarray}$

判別式が０になるところは極が２重解になるところですが、そこがシステムの挙動が変化する境目です。判別式が０になる $K_p$ や $K_d$ の値からそれぞれの値が少しでもずれると、極は２実数解か共役複素解になるわけです。

本考察では $K_p$ を変化させたときに $K_d$ をどんな値にすれば２重解になるのかを求めてみます。つまり判別式が０になる方程式を $K_d$ について解いてみます。以下の式が結果です。

$\begin{eqnarray} K_d=\frac{K_p x_{ms} \pm 2 \sqrt{K_p V}}{V} \end{eqnarray}$

以上から、実は２重解になる $K_d$ は２通りあることがわかりました。これを横軸 $K_p$ で縦軸 $K_d$ のグラフで表してみました。

青い線とオレンジ色の線上にある $K_p$ と $K_d$ の組み合わせでは極が２重解になります。

青い線より下の領域及びオレンジ色の線より上の領域の $K_p$ と $K_d$ の組み合わせでは極が２実数解になります。

青い線とオレンジ色の線に挟まれた領域の $K_p$ と $K_d$ の組み合わせでは極が共役複素解になります。

このグラフを参考にしつついろいろと $K_p$ と $K_d$ を変えてみて検討を行ってみました。

その際、オレンジ色の線上のゲインの組み合わせだと微分ゲインが大きいので速応性が下がると考えて最初から考えないことにしました。

青色の線上で $K_p$ を変えてそれに応じた $K_d$ の値でシステムのシミュレーションをしてみた結果が以下です。

重解になるゲイン設定で $K_p$ を大きくしていくとオーバーシュートがなくなります。即応性は若干悪くなりますが、なんとか０．１秒付近で目標値に行ってくれている様なきがします。（かなり希望的フィルターをかけた場合） $K_p=6000$ あるいは $K_p=8000$ で十分使えそうです。

ここで今度は $K_p$ を固定して $K_d$ を変えてみます。

$K_p=6000$ のとき青色の線上では $K_d=127$ ですこの値を挟んで $K_d=127$ を少し変えてみたものをいくつかシミュレーションして比較します。

どれも良さそうに見えますが、緑色の線が重解になる場合です。 $K_d$ が127より小さくなると応答は早くなりますがオーバシュートが大きくなります。また127より大きくなると応答が遅くなります。応答は遅くしたくないので、オーバーシュートが許容範囲ならば $K_d$ は大きくしたくありません。

この結果ならば、複素共役解の範囲に持っていってもそれほど悪い応答ではありません。しかし、計算でも求まる $K_d$ から微調整する必要もあまり無いようです。

線形シミュレーションと非線形シミュレーションの比較

ここまでは線形解析で作成した線形モデルに対してのシミュレーションでした。ここで、念のため線形化する前のモデルに対して同じ誘導則でシミュレーションを行い、線形モデルとの比較をしてみます。

ゲインは先ほどの最後の $K_p=6000$ の場合を試験しました。

両者は、ほぼ一致し問題ないことが確認できました。

センサ情報から位置の推定手法による違い

標題から内容を期待されると困りますが、最初の方で述べた、センサの距離情報からセンサ位置をどう割り出してフィードバックするかで結果に違いが出るかみていきます。

比較したいのは次の３つです。

センサの値をそのまま壁との距離として使用
センサの値をセンサの取り付け角で補正して壁との距離を算出
センサの値をセンサの取り付け角とロボットの方向をつかって壁との距離を算出（これまでの検討に該当）

以上の場合をシミュレーションで比較してみます。シミュレーションは誤差の微分をフィードバックする方法を適用しています。

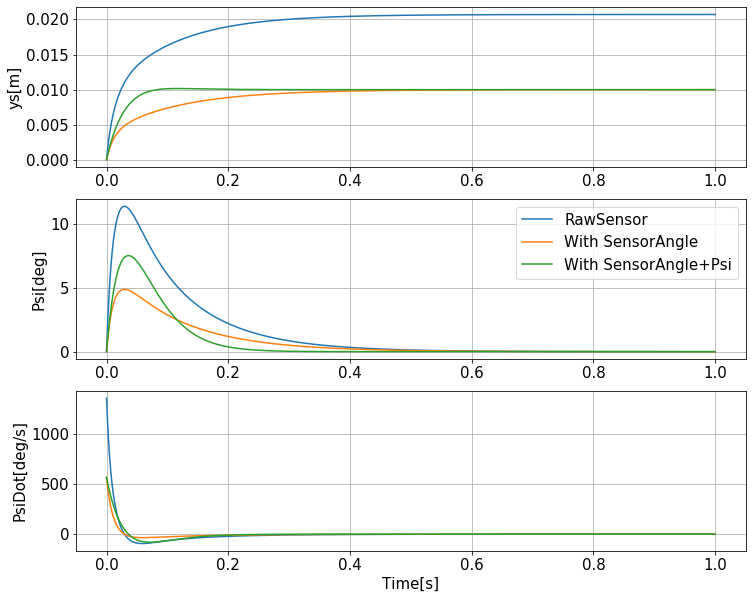
ゲインの設定は全て同じで先ほど決定したゲインを使用しています。

青色がセンサの情報をそのまま壁との距離とした場合です。取り付け角がある場合はセンサの壁との距離よりセンサ値は大きくなるので壁により近づかないと内部的には目標の位置にいないことになります。従って、計算結果のように大幅に目標位置よりズレたところに収束しています。また、この場合は目標角速度も大きく、大幅なゲイン調整が必要です。

オレンジ色はセンサの取り付け角でセンサ値を補正します。取り付け角は事前にわかりますので、これで補正することは容易ですが、簡単に実現できますが効果は大きく最終的にはロボットの位置も目標値に収束します。ロボットの向きは最終的に０になるので、取り付け角での補正が結果的に現実の値と一致するため最終的には目標位置に制御できます。

緑色は取り付け角と現在のロボットの方向で補正したものです。これまでの検討で行ってきたものはこれに該当します。結果はこれまでの検討と同じです。

ロボットの姿勢が推定できない場合もセンサの取り付け角を考慮してセンサと壁との距離を計算してやると思ったより良い結果が得られます。

いずれの手法でもロボットは壁にそって走行することができました。

おわりに

前回の記事に３週間に一記事ぐらいのペースでと書いたにもかかわらず、今回は約１ヶ月かかってしまいました。サボっていたわけではないのですが、中々筆が進まなかったのと、裏でやっている検算というか式の展開が間違い連発で思った結果にならなかったのが原因です。

ロボットを壁沿いに走らせるというのもちゃんと書こうと思うと、中々大変なものだなと痛感しました。適当にやってもそこそこ走るんですけど、やはり一度はきっちり取り組んでけりを付けたいところです。今回は机上検討のみでしたが、いずれ実機を用いた続きを書きたいと思います。

今回の記事ではロボットのダイナミクスは考慮していません。それを考慮しないと今回のようにきれいにはいかないはずなので、どこかで扱いたいなあと思います。

飛翔隊の誘導制御系の設計も誘導系の設計、制御系の設計を別々にやって、後から統合したりしてました。システムの中にロボットのダイナミクスを陽に入れてしまって、誘導系と制御系の設計を一緒に行うという研究もなされています。ミサイルのそれを修士時代のテーマとして扱ったこともあります。システムの次数がべらぼうに大きくなって「こりゃ現実にはむりだべ」と思いながら日夜Matlabと格闘していました。

今回の記事は時間をかけすぎたためか、最初と最後がつながっていないような気もします。さらには、いろいろ錯乱したためか言及しなくても良いことを書いているかもしれません。少しづつ手直していきたいと思っていますので、ご容赦ください。

参考文献

基礎制御工学増補版 (情報・電子入門シリーズ)

作者:伸明, 小林,亮一, 鈴木
発売日: 2016/03/09
メディア: 単行本

付録

計算に使用したコードの一部を付録とします。

誤差に比例して角速度指令

以下はゲインを少しづつ変えてそれぞれの計算結果を比較するのを自動的に行います。

#multi
import matplotlib.pyplot as plt
import numpy as np
from tqdm.notebook import tqdm as tqdm

'''
def rk4(func, t, h, y, *x)
ルンゲ・クッタ法を一回分計算する関数
    引数リスト
    func:導関数
    t：現在時刻を表す変数
    h：刻み幅
    y：出力変数（求めたい値）
    *x:引数の数が可変する事に対応する、その他の必要変数
※この関数では時刻は更新されないため、これとは別に時間更新をする必要があります。
'''
def rk4(func, t, h, y, *x):
    #print(t,h,y, *x, y)
    k1=h*func(t, y, *x)
    k2=h*func(t+0.5*h, y+0.5*k1, *x)
    k3=h*func(t+0.5*h, y+0.5*k2, *x) 
    k4=h*func(t+h, y+k3, *x)
    y=y+(k1 + 2*k2 + 2*k3 + k4)/6

    return y

'''
導関数の書き方
def func(t, y, *state):
    func:自分で好きな関数名をつけられます
    t:時刻変数(変数の文字はtで無くても良い) 
    y:出力変数(変数の文字はyで無くても良い)
    *state:その他の必要変数(引数の数は可変可能))
#関数サンプル
def vdot(t, y, *state):
    s1=state[0]
    s2=state[1]
    return t+y+s1+s2
    
'''
#以下ロボットの位置と速度を計算するためルンゲクッタソルバに渡す導関数
V_spec=0.8
xms_spec=0.04

def robot_set(V=0.8, x=0.04):
    global V_spec, xms_spec
    V_spec=V
    xms_spec=x

def robot_spec():
    global V_spec, xms_spec
    #移動ロボット
    #V=0.8
    #xms=0.04
    return V_spec, xms_spec


def ysdot(t, ys, psi, psidot):
    V,xms=robot_spec()
    return xms*psidot + V*psi

def psidot(t, psi, ys, K, yref):
    V,xms=robot_spec()
    return K*yref-K*ys

###################################
# main
###################################

N=5

Ys=[[] for _ in range(N)]
Psi=[[] for _ in range(N)]
Psi_dot=[[] for _ in range(N)]
T=[[] for _ in range(N)]

an=1000
bn=1000
Pstring='K'

for i in range(N):
    K=bn+an*i
    #K=1200.0
    robot_set()
    #robot_set(x=bn+an*i)
    t=0.0
    ys=0.03
    psi=0.0
    yref=0.04
    psi_dot=psidot(t, psi,ys,K,yref)

    #刻み幅
    h=1e-5

    for n in  tqdm(range(100000)):
        Ys[i].append(ys)
        Psi[i].append(psi*180/3.14159)
        Psi_dot[i].append(psi_dot*180/3.14159)
        T[i].append(t)


        oldpsi=psi
        oldys=ys

        psi_dot=psidot(t, psi,ys,K,yref)    
        ys  = rk4(ysdot, t, h, oldys, oldpsi, psi_dot)
        psi = rk4(psidot, t, h, oldpsi, oldys, K, yref)

        t=t+h
        #print('i omega',i,omega,e,TL)
    Ys[i].append(ys)
    Psi[i].append(psi*180/3.14159)
    Psi_dot[i].append(psi_dot*180/3.14159)
    T[i].append(t)

plt.figure(figsize=(7,6))    
plt.subplot(311)
for i in range(N):
    plt.plot(T[i], Ys[i], label='{}={}'.format(Pstring, bn+an*i))
plt.ylabel('ys[m]')
#plt.legend()
plt.grid()

plt.subplot(312)
for i in range(N):
    plt.plot(T[i], Psi[i], label='{}={}'.format(Pstring, bn+an*i))
plt.ylabel('Psi[deg]')
#plt.legend()
plt.grid()

plt.subplot(313)
for i in range(N):
    plt.plot(T[i], Psi_dot[i], label='{}={}'.format(Pstring, bn+an*i))
plt.xlabel('Time[s]')
plt.ylabel('PsiDot[deg/s]')
plt.legend(loc='upper right')
plt.grid()

plt.show()

誤差とその微分の両方に比例して角速度指令とする方法

import matplotlib.pyplot as plt
import numpy as np
from tqdm.notebook import tqdm as tqdm

'''
def rk4(func, t, h, y, *x)
ルンゲ・クッタ法を一回分計算する関数
    引数リスト
    func:導関数
    t：現在時刻を表す変数
    h：刻み幅
    y：出力変数（求めたい値）
    *x:引数の数が可変する事に対応する、その他の必要変数
※この関数では時刻は更新されないため、これとは別に時間更新をする必要があります。
'''
def rk4(func, t, h, y, *x):
    #print(t,h,y, *x, y)
    k1=h*func(t, y, *x)
    k2=h*func(t+0.5*h, y+0.5*k1, *x)
    k3=h*func(t+0.5*h, y+0.5*k2, *x) 
    k4=h*func(t+h, y+k3, *x)
    y=y+(k1 + 2*k2 + 2*k3 + k4)/6

    return y

'''
導関数の書き方
def func(t, y, *state):
    func:自分で好きな関数名をつけられます
    t:時刻変数(変数の文字はtで無くても良い) 
    y:出力変数(変数の文字はyで無くても良い)
    *state:その他の必要変数(引数の数は可変可能))
#関数サンプル
def vdot(t, y, *state):
    s1=state[0]
    s2=state[1]
    return t+y+s1+s2
    
'''
#以下ロボットの位置と速度を計算するためルンゲクッタソルバに渡す導関数

def robot_spec():
    #移動ロボット
    V=0.8
    xms=0.04
    return V, xms


def ysdot(t, ys, psi, psidot, yref):
    V,xms=robot_spec()
    return xms*psidot + V*psi

def psidot(t, psi, ys, Kp, Kd, yref):
    V,xms=robot_spec()
    return Kp/(1+xms*Kd)*(yref-ys) -V*Kd/(1+xms*Kd)*psi

###################################
# main
###################################

N=5

Ys=[[] for _ in range(N)]
Psi=[[] for _ in range(N)]
Psi_dot=[[] for _ in range(N)]
T=[[] for _ in range(N)]

an=2000
bn=2000
LString='Kp'

for i in range(N):
    Kp=bn+an*i
    #Kp=6000
    V,xms=robot_spec()
    Kd=(Kp*xms-2*np.sqrt(Kp*V))/V    
    #Kd=an*i+bn
    t=0.0
    ys=0.0
    psi=0.0
    yref=0.01
    psi_dot=psidot(t, psi,ys,Kp,Kd,yref)

    #刻み幅
    h=1e-5

    for n in  tqdm(range(50000)):
        Ys[i].append(ys)
        Psi[i].append(psi*180/3.14159)
        Psi_dot[i].append(psi_dot*180/3.14159)
        T[i].append(t)


        oldpsi=psi
        oldys=ys


        psi_dot=psidot(t, oldpsi,oldys,Kp,Kd,yref)
        ys  = rk4(ysdot, t, h, oldys, oldpsi, psi_dot, yref)
        psi = rk4(psidot, t, h, oldpsi, oldys, Kp, Kd, yref)
        t=t+h
        #print('i omega',i,omega,e,TL)
    Ys[i].append(ys)
    Psi[i].append(psi*180/3.14159)
    Psi_dot[i].append(psi_dot*180/3.14159)
    T[i].append(t)

plt.figure(figsize=(12,10)) 
plt.rcParams["font.size"] = 15
plt.subplot(311)
for i in range(N):
    plt.plot(T[i], Ys[i], label='{}={}'.format(LString,bn+an*i))
plt.ylabel('ys[m]')
plt.legend()
plt.grid()

plt.subplot(312)
for i in range(N):
    plt.plot(T[i], Psi[i], label='{}={}'.format(LString, bn+an*i))
plt.ylabel('Psi[deg]')
plt.legend()
plt.grid()

plt.subplot(313)
for i in range(N):
    plt.plot(T[i], Psi_dot[i], label='{}={}'.format(LString, bn+an*i))
plt.xlabel('Time[s]')
plt.ylabel('PsiDot[deg/s]')
plt.legend(loc='upper right')
plt.grid()

plt.show()