
はじめに
マイクロマウスの迷路探索では探索アルゴリズムとして左手法、トレモー法,足立法などがあるのですが そういった観点とは別に迷路をノードとエッジに見立てたグラフとしてとらえて、ダイクストラ法で 最短経路を見出そうというお話をしたいと思います。
前にも紹介していますが、 2003年に「3式」というマイクロマウスを開発しました2004年にはジャイロを搭載して「3式改」としました。 斜めに探索する「斜め探索」をさせようと意欲的に開発を進めました。オドメトリで自己位置推定してセンサー情報で 位置補正しながら走行するマイクロマウスができたのですが、どうもセンサー処理系が弱くて壁を誤って認識したり、 そのために補正が狂ったりして大会ではいい結果を残せなかったことが多かったのが残念です。


斜め探索のデビュー戦だった2004年の東日本大会の動画が見つかり、田代さんから「世界初の斜め探索」とのお言葉を頂いていたのが懐かしく、再度感激しています。 そのビデオでは最終トライはスタックして失敗するのですが、スタックしたあとに自動復帰を仕込んでいたのがうまく動いて、スタートに帰ってきています。 あまり多くを語らず黙々と大会に出場していたのですが、田代さんがそれに気が付いて「これは、スタート地点に戻ろうとしてるんですか?あそこで狂ってないんですね.」と聞かれていました。 何も話していないのにそれに気が付かれてそれを聞いていただけたのが有難く感謝しています。
次の動画は何度もアップしていて申し訳ないですが、全日本の予選です。 探索走行が一歩一歩だった地区大会から比べると、だいぶ連続走行に近い感じに進化しています。
こちらでも恥ずかしながら途中でクラッシュして、自動復帰が発動しています。 全日本の時は少し改良されていて、それまでやっていたことを続ける仕様に変更されています。 決勝のビデオも見つけてあるのですが、なんどもクラッシュして、完走できていなくて恥ずかしいのでお蔵入りです。
決勝で完走できていないのに「ニューテクノロジー賞」を頂けて本当にうれしかったのを覚えています。 表彰式の時は自分が呼ばれるとは思っていなかったので、心底驚きました。 ただ、僕は完全に自律的に一度も手を触れないで完走を目指しているので、いまだに心残りはありますので、いつか完全な目指すマイクロマウスを作りたいと思っています。
話はまた、昔の話になってしまいましたが「斜め探索」をするためには、従来からの区画単位の迷路データ管理では難しいと感じていました。 最短走行で斜めに走行できるのは連続する90度旋回が判明した後でそれを斜め45度走行に置き換えます。 探索時に前に行くか、左右に行くかそれらに加えて斜め45度に行くかを判断するためには、迷路の見方を変えなければなないと思い、壁のあるところを移動の目標点ととらえ、そして目標点に壁があるか無いかを記憶しようと考えました。
これが、壁があるところをノードとし、ノードとノードを繋ぐラインをエッジと捉える「グラフ理論」を勉強するきっかけになりました。
次の動画が、そのための探索アルゴリズムを確認するために当時作ったソフトを使って迷路にどのようにグラフを適用するのかを説明した動画になります。
グラフ理論
前振りが長かったですが、「グラフ理論」について簡単に触れたいと思います。 私は数学やアルゴリズムが専門ではないので、ロボットのために必要な部分だけかじっただけですので、 話はあまり当てにはならないかもしれませんが、マイクロマウスのプログラミングで経験したことや、 勉強したことを思い出しながら以下では述べたいと思います。

上の図に示したものを「グラフ」と呼びます。ほとんどの人が学校で習う「グラフ」とは違っています。ただおそらく根っこは同じで、図示して物事を判りやすくするツールと言うところは同じことだと考えられます。
グラフ理論において、図の丸を頂点又はノード(Node, Vertex)と呼びます。ノードとノードを接続する線を辺またはエッジ(Edge)と呼びます。 解説書には日本語の頂点と辺よりもノード、エッジを使っているほうが多いようですので本記事もノードとエッジと呼びます。
エッジの長さを重みと呼びます。長さと言いましたが物理的な長さと対応する必要は本当はありませんが、例えばノードが駅で、エッジが駅と駅の間の長さ(距離)と捉えると、グラフを見たときにイメージがわいてきます。
今の例のように本当の駅も複雑に駅同士が接続されており、どの駅を経由していくのが最も早いのかそのパス(道)を見つけたいことが良くあります。 グラフを用いてそのような問題を解いているのが乗換案内をするアプリケーションです。
マイクロマウスだけではなく迷路をグラフとして表して、探索問題を考えたり、最短経路を導出したりする問題が古くから考えられています。

サンプルとして上の迷路についてグラフを考えてみようと思います。スタート区画がSでゴール区画がGです。 上のような迷路はスタート区画とゴール区画の壁が繋がっていないので、左手法という壁に左手を当てながら歩く古典的な迷路解法ではゴールすることはできません。

簡単に迷路の区画の中心にノードを配置し、各ノードから行ける区画のノードにはエッジを繋げてみたのが上の図になります。ここでは簡単グラフと名付けたいと思います。
迷路を探索するロボットには最初はこのグラフが判りませんので、ロボットは自分の周辺の訪問できる区画を訪問しながら、訪問先の区画からさらに行ける区画を確認し地図を作りながら進みます。 これを探索と呼びます。探索とは上のような迷路では区画を訪問していくことですし、グラフで言えば、各ノードを訪問していくことになります。
それでは、どういう手順を踏めば、全ノードを探索することができるでしょうか。全ノードを探索できれば、その中に必ずゴールに到達することもあるはずです。
説明の都合になりますが、探索の前提として
- 迷路を探索する際に隣接する区画に行けるかどうかは判りますが、その先の区画は見えず先が知りたければ隣接区画を訪問しなければならない
- 訪問した区画には印をつけることができ、探検者は印を逆にたどり戻ることができる
実は迷路をどう探索すればいいかというのは基本的なところは 大きくは二つあり「深さ優先探索」と「幅優先探索」がそれです。 更に、もう一つ「順位優先探索」を加えてもいいと思います。 名前がいかついので難しそうですが、実は案外簡単です。以下で説明してみます。

まず、各ノードに番号を付けました。 これを使って以後説明します。
深さ優先探索
深さ優先探索は、今いる場所から行ける未探索のノードがあれば記録し、記録された最新のノードに進みます。 探索したら記録から削除します。 そうしますと、分岐に会ったら、どれかを選び、それを繰り返し、行き止まりに会うか、すでに探索したノードに会うかするまで先に「深く深く」探索を進めます。 行き止まり又は探索区画に出会ったら、直近の分岐までもどり、まだ選択していないノードに進み、同じことを繰り返していく方法です。
具体的に上の迷路で説明しましょう。 ノード0のスタート区画では、前にしか進めませんので、前の区画を訪問します。 ノード4、ノード8と進んで初めて分岐に出会います。
分岐に出会ったときに、今は適当にどちらに行くかを決めることにします。 どちらに行くかを決める手順がロボットごとにあり、それによってロボットの性格が変わります。 この話についてはまた、別にしたいと思います。

そこで、ノード12を訪問することにしましたが、そこが行き止まりだという事が判りました。 ノード8に戻り、まだ訪問していないノード9を訪問します。
ノード9でまた分岐があるので、適当に選びノード13に進みます。 しばらく道なりにノード6まで進むと分岐にであい、ノード10を選ぶとゴールしたことになります。 今はゴールより全部のノードを訪問するのが目的ですので、行き止まりに来たら、直近の分岐のノード6に戻ります。

先ほど選ばなかったノード2に進むと分岐ですので、ノード1を選ぶとしばらく道なりでノード5で次のノードがノード9だと判りますが、ノード9は既に探索している既探索ノードです。 そこで、直近の分岐であるノード2まで戻ります。
ノード2で先ほど選ばなかったノード3に進みますが、ノード3を訪問するとすべてのノードを探索したことになるので終了です。
幅優先探索
幅優先探索は、探索したノードから行ける未探索のノードを記録します、記録した最も古いノードを最優先に探索します。探索し終わったら記録を削除します。もっとも古い未探索のノードを探索するまでは先には進まず、場合によっては戻りながら最初の場所から徐々に探索したノードを広げていく方法です。
こちらについては、訪問順を示すのみに留めますが皆さん自分で追ってみてどのようなものか確認してみてください。

幅優先探索の訪問の例
0→4→8→12→9→13→5→14→1→15→2→11→3→6→7→10
こちらは単独だと、来た道を戻る回数が多くなり移動距離が長くなる傾向があります。 複数の探検隊で手分けして行うのに適した方法です。
スタックとキューについて
深さ優先探索と幅優先探索の実装を考える際のポイントは各説明にありました探索可能なノードの記録と、記録されたノードをどういう順番で取り出して、取り出されたノードに進むのかが重要になります。 二つの探索方法の違いは実は記録からの取り出し順番だけになります。
アルゴリズムとデータ構造を語る際の用語にスタックとキューというものがあります。 これらが、データの取り出し方を表す重要な考え方となり、深さ優先探索と幅優先探索はスタックを使うのか、キューを使うのかという違いになります。


スタック
スタックと言うのは後入れ先出し(LIFO:Last Input First Output)と呼ばれ、最後に入れたもの(情報)を先に取り出します。本を積んでいくと最後に積んだものから手に取ることになるので、本を積んで取り出すイメージにこれは合います。
深さ優先探索では、新しいノードに行くたびに次に行くことが可能なノード番号をスタックに積み上げます。 そして、すぐに一番上にある番号は取りだしその番号のノードに行きます。これを繰り返すと深さ優先探索が完了します。スタックを使うと実にシンプルです。 新しいノードを探索した時にスタックすべきノードが複数ある場合は何らかのルールで積み上げる順番を決めます。
キュー
キューと言うのは先入れ先出し(FIFO:First Input First Output)と呼ばれ、先に入れたものから先に取り出します。待ち行列は先に並んだ人から順番が回ってきます。このイメージがキューのイメージです。
幅優先探索では、新しいノードに行くたびに次に行くことが可能なノード番号をキューに並ばせます。そして早く並んだものから取り出しその番号のノードから探索していきます。 こちらも並ばせる番号が複数ある場合は何らかのルールで並び順を決めます。
データの構造
ノードとノードの接続状況をどのようなデータ構造で表すかが問題になります。 マイクロマウスの場合は壁の情報をもった地図情報があればそこから逐次、接続状態を調べることができるので明示的に接続情報を保持する必要は無いといえます。 通常のグラフを使ったプログラムでは
- 隣接行列
- 隣接リスト
が使われます。
隣接行列

隣接リスト
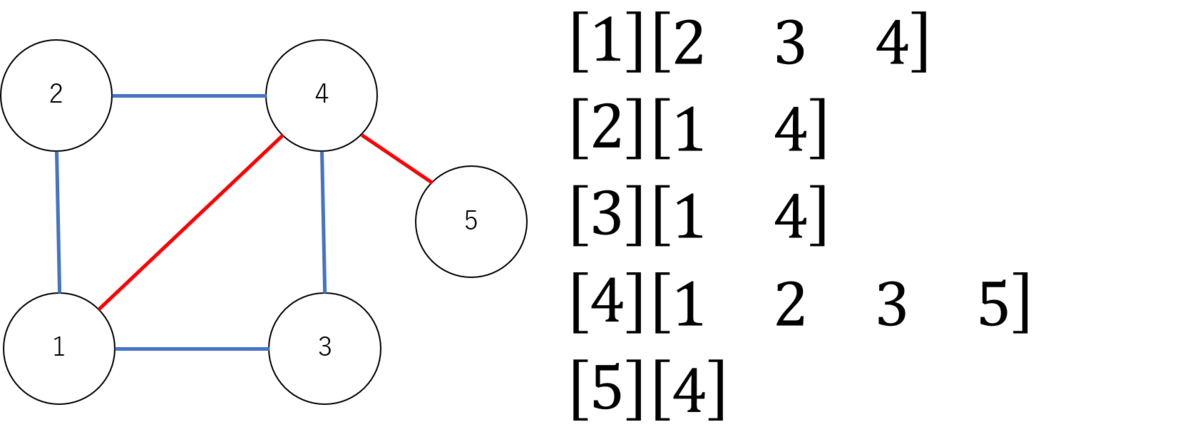
もう一つの隣接リスト表現と言うのは、ノードN番に隣接しているノードのリストの事です。 すべてのノードについて隣接しているノードのリストを作って保持します。 隣接リストをロボットのプログラムでは多く使われているC言語では配列を使った表現では隣接リストを表現するのはつらいです。 何故かというと、2次元配列で表現しようとすると、c言語の2次元配列は行列とみなせますから、ノードの数だけ行を用意できます。ここで隣接リストを表現しようとすると、列に隣接ノードの番号を入れようとすると思いますが、配列だと列数は固定で、考えうる最大の隣接ノード数まで確保しなければなりません。隣接ノードが一個だけでも使わない領域を確保しなければならないので通常の配列で隣接リストを表現するのであれば隣接行列にするれば良いと思います。
C言語で効率よく隣接リストを作る場合は連結リストを使います。本記事では連結リストの説明をし始めると大幅な脱線になるので今回はしないことにします。 気になる方はWikipediaにある記事を参考にしてみてください。C言語での実装例も最後に掲載されています。
探索をPythonで実験
Pythonで簡単な探索プログラムを書いて試してみようと思います。
Pythonは軽く思考を整理してコードに書いて試すのにも手軽で良い言語だと思っています。 シミュレーションの様に大量の反復をさせたりすると実行速度が気になってきますが、アルゴリズムの検証でそこにぶつかったら そこだけCやC++に置き換えるなどを検討するといいと思います。
Pythonの配列であるリストはリストの中にリストを入れられ、リストの中に入っているリストの次元が全く異なっていてもかまわないという仕様です。 ここは、大幅にC言語の配列と異なっています。
隣接リスト表現を実現するにはPythonのリストを使って実現しようと思います。 Pythonでも連結リストを作ることができるのでC言語と同じようなコードスタイルでもかけると思いますが、今回はロボットに移植しようと思っていないので、お手軽な方法でやろうと思います。
まず探索する迷路は先ほども出したものです。

この迷路を表すグラフをPythonで隣接リスト表現してみました。
g=[[4],#0 [2, 5],#1 [1, 3, 6], #2 [2], #3 [0, 8], #4 [1, 9], #5 [2, 7, 10], #6 [6, 11], #7 [4, 9, 12], #8 [5, 8, 13], #9 [6], #10 [7, 15], #11 [8], #12 [9, 14], #13 [13, 15], #14 [11, 14], #15 ]
簡単ですね・・・
リストの中に、長さの違う複数のリストを入れるといった形で簡単に実現してみました。
スタック又はキューの実装については、まずそのためのリストを用意します。 最初の要素はスタート地点となるのでスタートのノード番号0を入れておきます
stackorque=[0]
探索して、隣接するノードが見つかったら順にこのスタック又はキューを表すリストにそれらの番号を付け加えていくのでpythonのリストのメソッドのappendを使います。 例えば変数kに入っている値をおしりに付け加えたいならば
stackorque.append(k)
とします。
そうして、これを取り出すときに、最後に追加したお尻から取り出すとスタックになり、一番先頭から取り出すとキューになります。
まずスタックとして取り出す場合ですが
stackorque.pop(-1)
pop()と言うメソッドは指定した位置の要素を取り除きます。戻り値は取り除いた要素です。 -1は最後という意味で、リストの要素数が判らなくても-1を指定すると最後の一つを指したことになります。便利ですね。
つづいて、キューとして取り出す場合です
stackorque.pop(0)
データはお尻に追加されているので一番古いのは先頭にあるデータなのでpop(0)で先頭のデータを取り除きます。
これらを使って探索を実験するコードが以下です。
#グラフ理論 # 深さ優先探索と幅優先探索 #迷路を表すグラフの隣接リスト表現 g=[[4],#0 [2, 5],#1 [1, 3, 6], #2 [2], #3 [0, 8], #4 [1, 9], #5 [2, 7, 10], #6 [6, 11], #7 [4, 9, 12], #8 [5, 8, 13], #9 [6], #10 [7, 15], #11 [8], #12 [9, 14], #13 [13, 15], #14 [11, 14], #15 ] #各ノードに行ったかどうかチェックを付けるためのリスト check=[0]*16 #スタックかキューとして使うためのリスト stackorque=[0] #何個ノードを探索したかカウントする変数 counter=0 #スイッチ変数 # sw=0:幅優先探索 # sw=-1:深さ優先探索 sw=-1 #探索ループ while(counter<16): #スタックまたはキューからノード番号を取り出す node=stackorque.pop(sw) #探索したとして記録する check[node]=1 #そのノードの隣接ノードをすべてスタックまたはキューに追加する for k in g[node]: if check[k]==0: stackorque.append(k) counter+=1 #何か所目の探索かと探索したノードの番号を表示 print(counter, node)
変数swを変えるとpopで取り出す場所を指定できるので、同じループプログラムで深さ優先探索と幅優先探索が確認できます。 言い方を変えると、スタックを使うか、キューを使うかで探索の仕方が変わることを示せます。
変数swを-1にして深さ優先探索にしてみた結果です
1 0 2 4 3 8 4 12 5 9 6 13 7 14 8 15 9 11 10 7 11 6 12 10 13 2 14 3 15 1 16 5
右の数字がノード番号で上から順に見ていくとどの順番でノードを訪問しているか判ります。 実際の迷路探索では戻るときに一度通ったノードを通らなければなりませんが、この実験ではその様子は示されません。 ここで示されたのは目指すノードがどの順で出てくるかを示しています。
ちょっと先ほどの解説と違うんですが、複数の候補からどれを先にするかの決め方がプログラムでは違うので少し違った結果になります。 (さて、どこを変えたら解説と同じ動きになるでしょうか?)
以下は、今度はswを0にして幅優先探索の結果です
1 0 2 4 3 8 4 9 5 12 6 5 7 13 8 1 9 14 10 2 11 15 12 3 13 6 14 11 15 7 16 10
今プログラムは、侵入できない区画があるとループの回数を変えなければならず、本当の探索ではそれは探索するまでわからないはずなので、そこは手を抜いています。 深さ優先探索と幅優先探索の動きを確認するための簡単プログラムという事で手抜きをお許しください。
順位優先探索
3つ目の順位優先探索を説明します。これまで次の訪問ノードの候補を新しいノードを訪問するたびにをスタックやキューに記録し、それぞれに応じて取り出すことによって「深さ優先探索」または「幅優先探索」になるという説明をしてきました。 記録されたノードを取り出すルールにLIFOまたはFIFO以外を当てはめ、何らかの方法で優先順位を付けると「順位優先探索」になります。 優先順位がつけられるデータが入ったデータ構造を順位キューと呼びます。
順位の付け方の例としては、ゴールから最も近いノードを優先するなどです。
この方法が最も汎用的で、優先順位をスタートから最も近いノードにすると次に話すダイクストラ法による、最短経路の導出になります。
ダイクストラ法
マイクロマウスは探索ができたとしても、最短経路を見つけられないといけないので、どうやって最短経路を見出すかが問題です。 簡単で確実な方法は、迷路に沿ってゴールからの歩数を数えます。スタートまで数え終わったら、逆に歩数が減っていく方向にスタートからたどると、それが最短経路となります。 この方法は区画から区画への移動(ノードからノードへの移動)を一歩として行う方法です。
これを汎用的にしたのが最短経路導出アルゴリズムとして有名なダイクストラ法です。
ダイクストラ法はノードとノードの距離(重み)を1に限定せずに、任意の正の重みで最短経路を求めることができます。
以下、ダイクストラ法について説明します。
まず前提として
- ノードとノードのエッジには異なる重み(距離)があるとします
- 説明の中で値(スタートからの距離)を記録する記録先をデータ構造と呼びます
- 記録する際には、値とその値が示しているノードとの対応が後からでも判るとします
では、手順を説明します
- スタートノードに接続しているすべてのノードのスタートノードからの距離を求め記録します
- データ構造から最小値をもとめます。最小値の示すノードを次の訪問先として選びます。その際、最小値はデータ構造から取り除きます.
- 新たな訪問先のノードに接続している未訪問のすべてのノードのスタートからの距離を求め記録します。その際、すでに以前に距離が計算されていた場合は、最新の計算結果が小さい場合だけ記録します。
- すべてのノードを訪問したら終了。そうでなければ2.に戻ります。
ダイクストラ法の実装方法には主に二つがあります。
実装の方法①
グラフ表現のグラフは隣接リストを用いて表現し、データ構造として、順位キューを用います。最短距離のノードを見つける際は、順位キューでソートを行って決定します。 ノードの数に比べてエッジの数が少ない場合はこちらの方法が早く終了する可能性が高い。
実装の方法②
すべてのノードについて順番に、訪問済みか、訪問済みでないか、未訪問で現在の訪問ノードに隣接しているならばスタートからの距離を計算し、さらにこれまでに計算した距離の中で最小値であればそれを記憶し、すべてのノードにこれらの操作が終わったならば、最小の距離のノードを次の訪問ノードにする手順を繰り返す。これは総当たり的な方法となりますが、ソート作業をしなくて済みます。
なお、参考文献「アルゴリズム in C 第3巻」では方法①は「順位優先探索」で方法②を「ダイクストラ法」としています。
以上の説明を動画にしてみましたのでご覧ください。
斜めに探索させる仕組み
迷路の大きさとロボットの大きさが許せば、いつも縦横方向に走行する必要はないはずです。マイクロマウスにはスラローム旋回と言って、速度を持ちながら旋回時に滑らかに方向を変えながら走行する方法があります。 その際においても、探索時は旋回が終わると縦か横方向に向くことを繰り返して迷路を探索していきました。
グラフで考えると、グラフの構造が前出の簡単グラフでは次に行く区画は、隣接する前の区画か、左右の区画しかないため、自然と縦と横方向への移動に限定されます。
グラフを想定していないソフト設計においても、大体は簡単グラフを考えた設計と酷似しているはずですので、それらの設計方法では斜め方向への選択は出てきません、無理にやろうとするのは労力に見合わないばかりかおそらくバグの温床になります。
そこで、斜め方向に移動することも考慮してソフトを作ろうとしたときにノードの位置を壁の位置にずらして配置してみました。

上の図がそのサンプルになるのですが、これにすることで、探索時に斜めの位置にある場所を目指すことができるようになります。
しかし、目指す場所として斜めの場所を選択できるようになることと、斜めの場所に移動できることとは別問題です。 通常両壁を見ながらロボットの位置を壁の中心に修正しながら走っているマイクロマウスでは斜めに走っている期間が長くなるとずれを修正することができずにスタックする確率がどんどん上がります。
この方式の欠点は迷路の区画の中心を目指さないことです。 2004年の予選の動画のゴールした状態を確認していただければわかるのですが、区画と区画の間の本来壁が置ける位置にゴールして止まっています。 この場合、区画の中心に止まることは特殊な場合となるため、すこしイレギュラーなコードを書かなければならず、 2004年の東日本大会の斜め探索デビュー戦の動画を確認すると、途中でスタート地点に帰れないバグが発生しています。
もしかすると、今後メモリ等の容量が許せば、柱の位置にもノードがあることになる、次の図のようなイメージで実装をするかもしれません。

おわりに
長い割には、実際のロボットにはどう使ったらいいのかいまいち判らない感じの記事になってしまいました。 本当は迷路探索のシミュレーションをPythonで実装して見せようと企画していますが、もう少し時間をかけて記事をブラッシュアップしていこうと思っています。
今回はマイクロマウスの迷路探索にからめた話なのに「拡張左手法」や「足立法」の話は一切していません。すみません。
結局のところ、どんな方法をとれば一番いいのか?
所詮迷路の先はどうなっているのかわからないし探索では実はゴールが最優先ではないような気がします。 とはいっても目の前にゴールがあったらとりあえず入っておこうという気にはなります。 基本的には「深さ優先探索」をアレンジすれば良いのではと思うこの頃です。 まあ、最近は「足立法」みたいなものばかり実装したり、 分岐でランダムに行き先を決める手抜きのアルゴリズム入れたり遊んでましたので またシミュレーションからまじめに取り組めたらいいと思います。
斜め探索にしても、まだやりたいことができていないのと、 しばらく時間を空けてしまって探索アルゴリズムも忘れかけていたので、 今回これを書いている途中で、だいぶ前に書いたプログラムを探し出して見直したり、 動画を発掘して見たり自分で楽しめました。 まだできていないことがたくさんあるので、 少しづつでも自分のマウスに実装して良ければ良いなと思っているところです。
そうそう、YouTuberもどきで遊んでみたのも楽しかったですよ。 本ブログ記事全記事をYouTubeにしてみるとか(笑い) 老後の楽しみとしますか・・・
では、また!