２体問題のシミュレーション

f:id:kouhei_ito:20200325064952p:plain

はじめに

前回ウイルス感染のパンデミックのシミュレーションをしてみたのですが、粒子のクラスを一般的な移動のシミュレーションに使えそうなのですこし、改良して使ってみようかなと思いました。

数値計算を考えるときに２体問題は解析的に解けるけど３体問題は解析的に解けないのでコンピュータでの計算が必要ですが、今日はまず練習として２体問題を解く計算をしてみました。

blog.rikei-tawamure.com

万有引力

地球を回る月の運動のシミュレーションをしようと思います。

問題を簡単にするために地球は止まっているものとします。

２物体は万有引力によって引き合います。地球と月ぐらいの大きさになるとそれなりに大きく、月が地球の周ることになります。

万有引力の大きさ

万有引力はお互いの質量 $m_1$ 、 $m_2$ の積をお互いの距離 $r$ の２乗でで割ったものに比例します。比例定数 $G$ を万有引力定数と呼びます。

$\displaystyle{ F=G\frac{m_1 m_2}{r^2} }$

地球と月の諸元

Wikipediaより

	地球	月
質量(kg)	$5.972\times10^{24}$	$7.348\times10^{22}$
半径(km)	$6357$	$1737$
公転半径(km)	$1.496\times10^{8}$	$3.844\times10^{6}$
公転速度(km/s)	$29.78$	$1.022$

さて、上の表にある月の質量と距離を用いて万有引力の大きさを計算してみると

$1.98\times10^{20}$ (N)

となり物凄い大きさで、地球と月は引っ張り合っていると言うことです。

ただし、この大きさで引っ張られても、月に生じる加速度はこれを月の質量で割りますので

$2.70\times10^{-4}$ (m/s²)

と非常に小さな値となります。

万有引力の向き

万有引力の式からでは万有引力の大きさのみ求められて、その力の向きがわからないと思います。

力は本来大きさと向きを持つ量なので、力が作用した物体がどっちに動くのかしりたいので力の向きが重要になります。

では、万有引力の力の向きはどうかと言いますと、互いに引き合いますので、月から見れば、地球の見える方向に引っ張られると言うことになります。

f:id:kouhei_ito:20200325203808p:plain — 万有引力の方向

万有引力ベクトル

計算的には方向と大きさが一緒になった万有引力ベクトルが求まるのがベストなので

万有引力の式から大きさを求める
月から見た地球の位置ベクトルを求める．地球位置ベクトルー月位置ベクトル
月から見た地球位置ベクトルの大きさを求める
月から見た地球位置ベクトルをその大きさで割り，単位方向ベクトルを求める
単位方向ベクトルに万有引力の大きさをかけて，万有引力ベクトルとする

以上の手順で万有引力ベクトルが求まりました．

月の運動

それでは，月の初速とおなじみの運動方程式

$\displaystyle{ m \frac{d \vec v}{dt}=\sum \vec F }$

位置と速度の関係

$\displaystyle{ \frac{d \vec x}{dt}= \vec v }$

これらをルンゲ・クッタ法を用いて数値解を求めていきます．

ルンゲ・クッタソルバーを当ブログでも以前作ってみましたのでそれを使おうと思います．

blog.rikei-tawamure.com

月の軌道上に最初から月の公転速度で動いている場合

これは，普段通りの状態が初期条件の場合です．当然円運動します

f:id:kouhei_ito:20200325205601g:plain — 月の周回運動

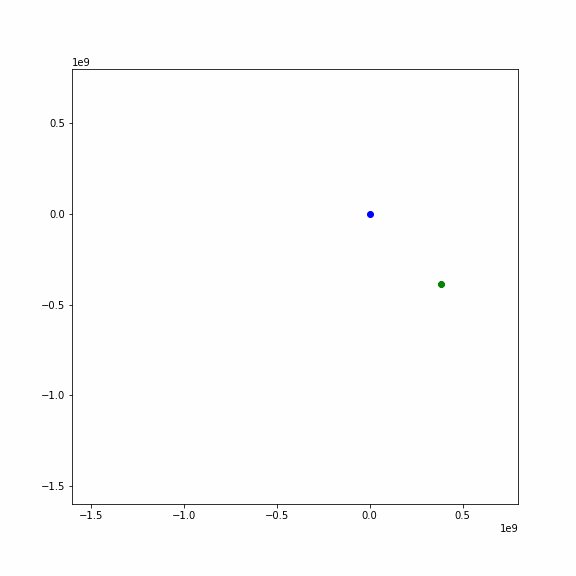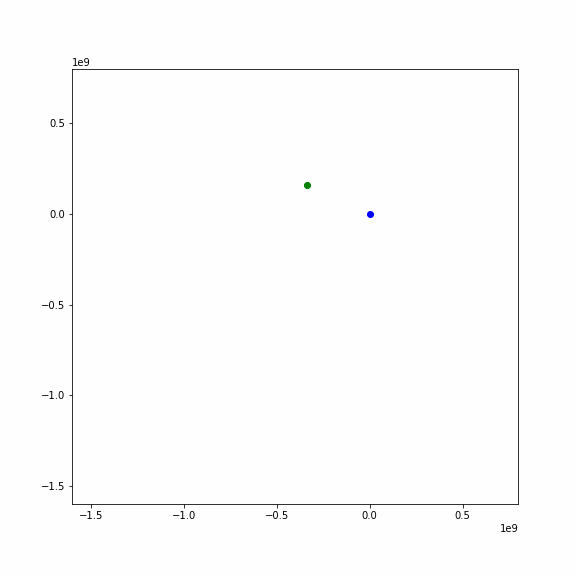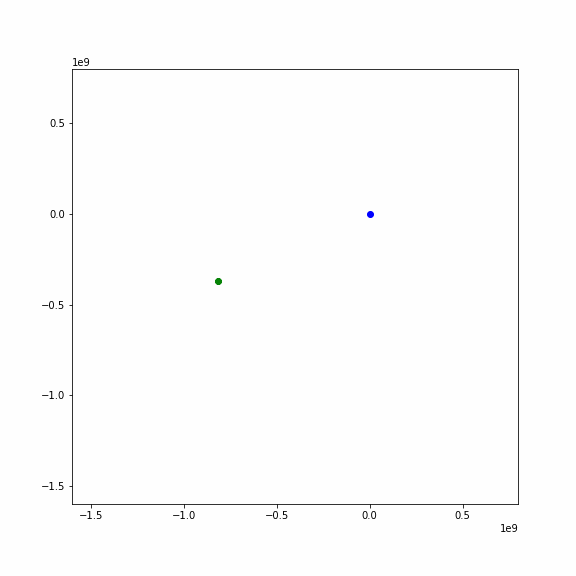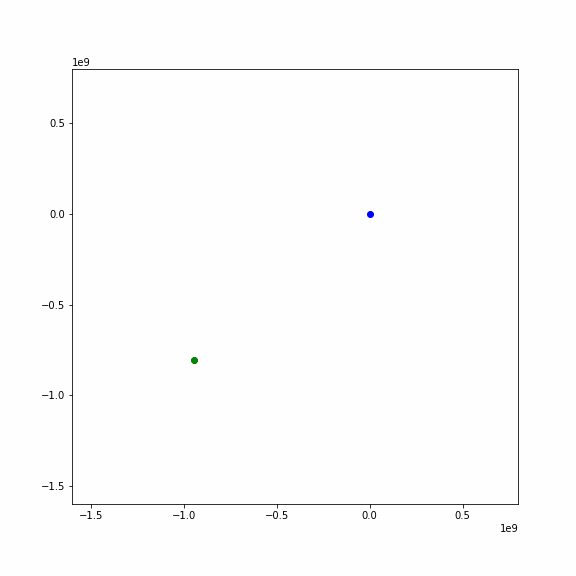
月の公転軌道から離れた位置から月が飛んでくる場合

カメラをちょっと引いて，広い範囲が映るようにしました．

あらら，地球にとらわれて衛星になるかと思いきや，フライバイして宇宙のかなたに行ってしまいました．

ちょっと角度が変わると，衛星にならず，地球にひかれて方向は変わりますが，アニメのようにどこかへ行ってしまいます．このとき，地球の重力で加速して速度を増します．これをフライバイと言って，宇宙探査機が燃料を使わずに軌道を変更し，増速するのに使われます．

f:id:kouhei_ito:20200325213021g:plain — 月のフライバイ

以上のコードを置いておきます

github.com

おわりに

若干，尻切れトンボで，説明足らずの回になってしまいました．時間ができたら，加筆修正したいと思います．

いろんな入射角で月を地球に突っ込ませたりして，楽しみます．

では，また！

理系的な戯れ

理工学系とくにロボットやドローンに関する計算・プログラミング等の話題を扱って、そのようなことに興味がある人たちのお役に立てればと思っております。