はじめに
こんにちは、こうへいです。
近頃はAIや機械学習が話題にならない日はない感じとなりましたが、AIの中身を知る人はほとんどいないと思われます。
かく言う僕もその一人ですが、多くのAIの中身はニューラルネットワークであると言われています。
それなら、20数年前Matlab/Simulinkでポチポチ作って卒論書いたなあと思い起こし、 何が変わったのかと、すっかり忘れてしまったことを思い出そうと思います。
タイトルは「アンドロイドは電気羊の夢を見るか」のパクリで、あんまり本文とは 関係がありませんが、AIで使われるニューラルネットワークは 脳の神経細胞のニューロンを模倣していますので、夢も見るのかとふと考えたりしています。
以下は今のところ、ぼくなりのまとめでもあり、理解が間違っている可能性は十分にあるので お気をつけください。
- ニューラルネットワークでできること
- ニューラルネットワークとはどうなってるのか
- 学習とはどんなことなのか
それでは、ニューラルネットワークワークに再入門しようと思います。
機械学習の問題
ニューラールネットワークによる機械学習はデータを与えることで学習をして、 「分類問題」と「回帰問題」に答えを出す事ができます。
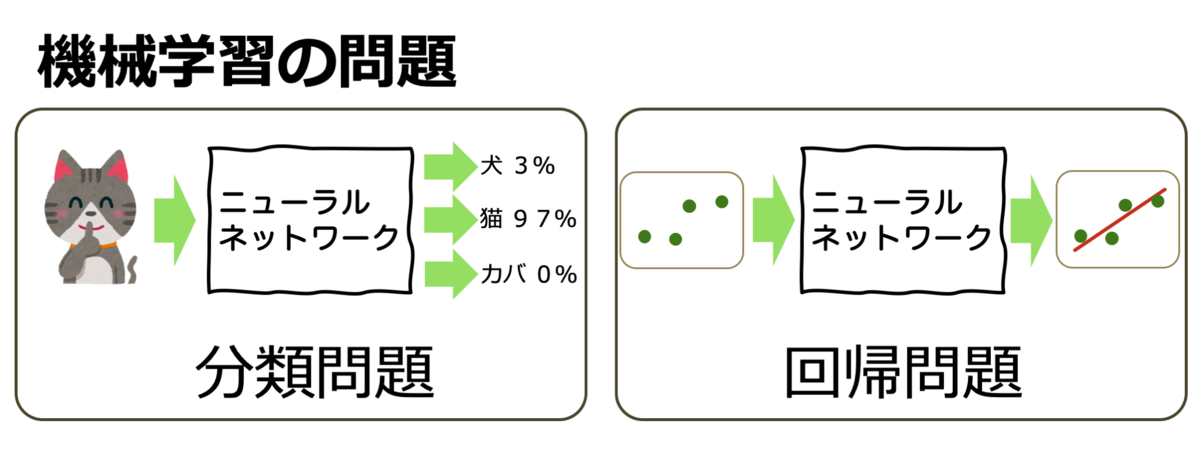
分類問題は図の例の様に何かの画像からそれが何であるのかを分類します。文字の認識などもこれにあたります。
回帰問題は説明が難しいですが、図の様にデータの集まりからその傾向を取り出すことにより、次のデータを予測するなどに用います。
人工ニューロン
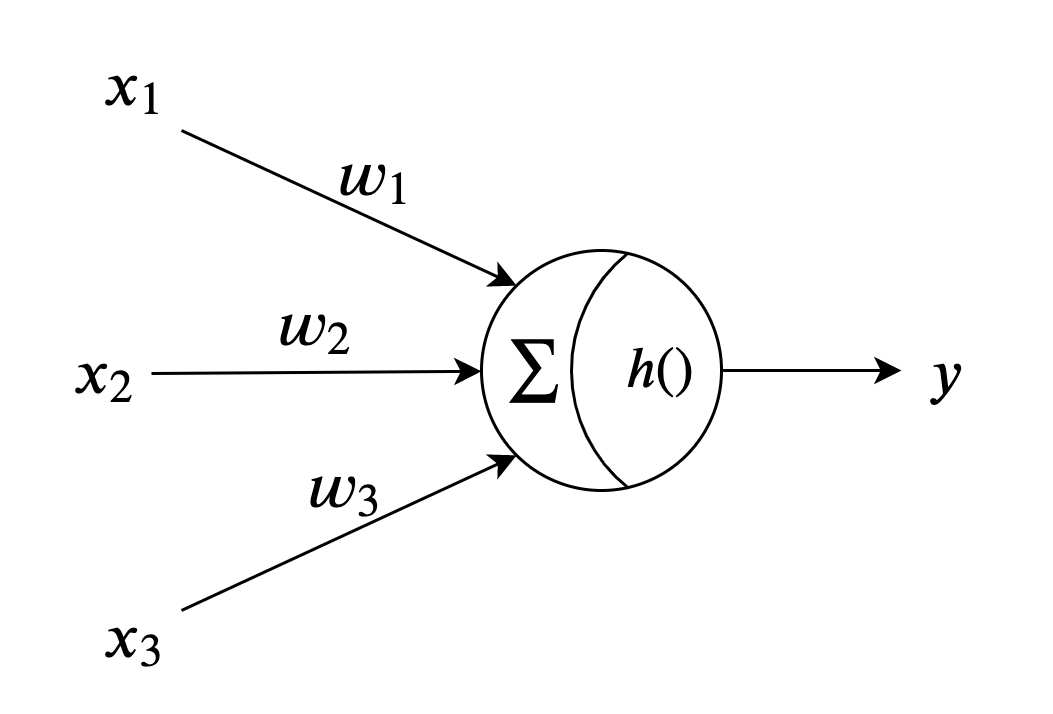
ニューラルネットワークは上図の様な神経細胞のニューロンを模倣した人工ニューロン(以下ニューロン)を複数接続したものになります。
図の丸をノードと言います。ネットワークを図示するときは、丸の中などを描かないで省略します。
この図ではニューロンに3つの信号が入っていきますが、この数は決まっておらず複数を入力する事ができます。
図の1個のニューロンは以下の数式を表しています。
各記号の意味は次の様になります
| 記号 | 意味 |
|---|---|
| 入力 | |
| 重み | |
| 出力 | |
| 活性化関数 |
計算式が示している事について説明してみます。
重み付け和
入力には重み
がかけられます。それを重み付けされた入力と呼びますが、
重み付けされた入力の全ての和を計算しています。これを、重み付け和と呼びます。
活性化関数
重み付け和の大きさによってニューロンがどの程度活性化するのかを示すのが、活性化関数です。 主に、あるのが
- ステップ関数
- シグモイド関数
- ReLU関数
のようです。
ステップ関数
重み付け和が閾値より小さければ0、大きければ1の様なステップ上の関数を選んだニューロンで構成されたネットワークをパーセプトロンとよびます。歴史的にはパーセプトロンが先にあり、その後ニュラールネットワークが研究されたとのことです。
シグモイド関数
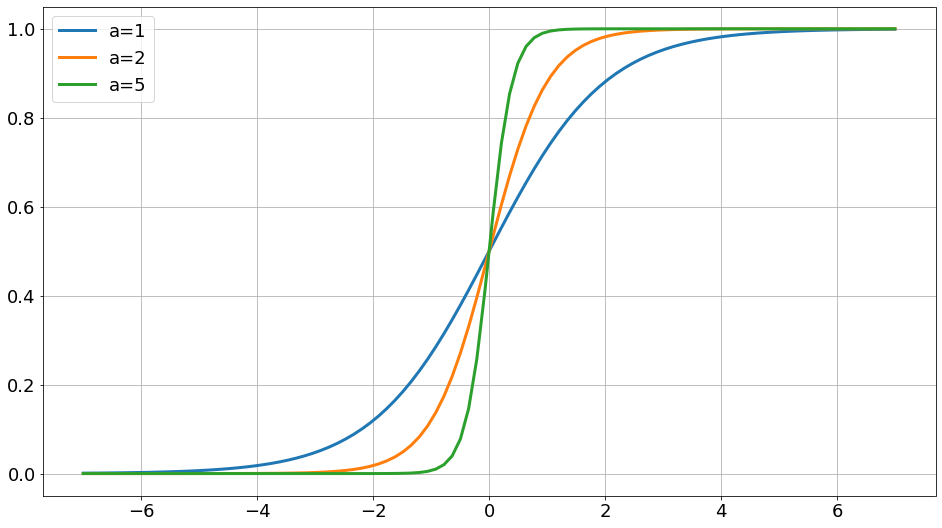
ステップ関数は非連続な関数で取り扱いが難しいので以下の式で表される、シグモイド関数を使う事が多いそうです。大昔もこれを使って作った記憶があります。
シグモイド関数の形は下図の様になり、係数を変える事で、急峻に切り立った形になっていきます。
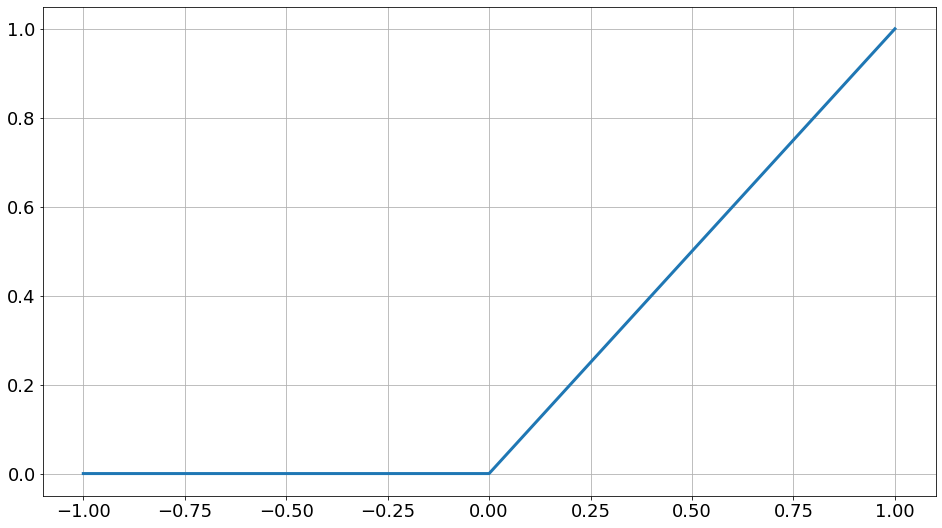
ReLU関数
これは再勉強して知った関数ですが、最近は下図の様な形になる、ReLU関数(ReLU:Rectified Linear Unit)が用いられる事が多く、良い結果を残しているそうです。2011年頃になって使われ始めたらしく、90年代に勉強していた僕は知らなかったわけです。 不勉強ですが、0のところで不連続になるところはうまく取り扱えるのか疑問で、もう少しこれを使った理論展開については追いかけないとならないと思っています。
ニューロンに表現できること
ニューロンは重みの値やその組み合わせを変える事で様々な関数を表現することができますが、一つだけでは表現できない関数もあり限界があります。
そこで、複数を組み合わせネットワークを作ることにより、様々な関数を表現する工夫があらわれました。
ニューラルネットワーク
ニューラルネットワークの構成
ニューラルネットワークは複数のニューロンを多層にわたって接続しネットワークを構成したものです。
ニューラルネットワークで表現できること
複数のニューロンを多層に接続する事で様々な多入力、多出力関数を表現する事ができます。
重みの決定の難しさ
11個のニューロンでも27個の重み
図に例ではニューラルネットワークは11個のニューロンが存在していて、 27個の重みがあります。意図した関数を作るためには27個の重みの値を決めなければならず 人間が手計算や試行錯誤で決めるには限界を感じます。
層数が増えると重みも指数関数的に増える
たとえば、手書きの数字を当てるニューラルネットワークを考えてみると、手書き文字を少なくとも8×8のマスの画素に分解したとしても、画素数は64個あります 64個のニューロンを3層にわたって構成すると64×64×64個の重みの決定が必要でもはや不可能となります。
どの層のニューロンの個数を何個にするかは決まっていないので一概にこの数になることもないのですが、 主に画像認識の分野での活用が目覚ましいので、入力変数の数は画素数ということもあり巨大な重み空間が生成されます。
学習とは重みの更新
学習とはニューラルネットワークの重みを正解に近づく様に更新していく作業です。
学習の種類
機械学習には「教師あり学習」「教師なし学習」「強化学習」の3つがあります。人工知能や機械学習を勉強したい人は 徐々にこれらの3つがどういうことなのか紐解いていかなければなりません。
教師あり学習
僕が勉強したのは「教師あり学習」に相当するので、今日は「教師あり学習」について概略を話したいと思います。
「教師あり学習」によって、冒頭で紹介した「分類」と「回帰」が達成できます。
「教師あり学習」の過程においては、先生が結果が良いのか悪いのかまず採点してくれます。
実際に採点をする先生は評価関数です。評価関数Jは以下の様な式です
正解はあらかじめ与えられているので変わりませんが、出力は同じ入力に対しても、重みの値が変われば変わります。
従って、評価関数Jは重みの関数という事ができます。
評価関数が0ならば完全に一致していることになるのですが、0にならなくてもできるだけ小さければ成績が良いということになります。満点は取れないけれど、なるべく上位の成績を目指します。
すると学習の目標は評価関数を最小にする重みを見つける最小値問題になります。
最小値問題、最大値問題の一般的な話
最小値や最大値になるパラメータを見つける問題は、変化する関数をパラメータで微分して、微分した結果が0に なるようにパラメータを決定します。
学習の評価関数を最小にする重み(重みがパラメータ)を見つけるのも評価関数を重みで微分します。
パラメータがたくさんあると、一つ一つのパラメータに対しての微分がでてきます。
複数の微分の値を0にする複数のパラメータを求めることになり、 比較的幸運ならば、巨大な連立方程式を解く事でパラメータが見つかることもありますが そうでない場合も多いです。
不幸にもパラメータが見つけれれないときの方法の一つに勾配法があります
勾配法
勾配法を説明するしょぼい絵を描いてみました。
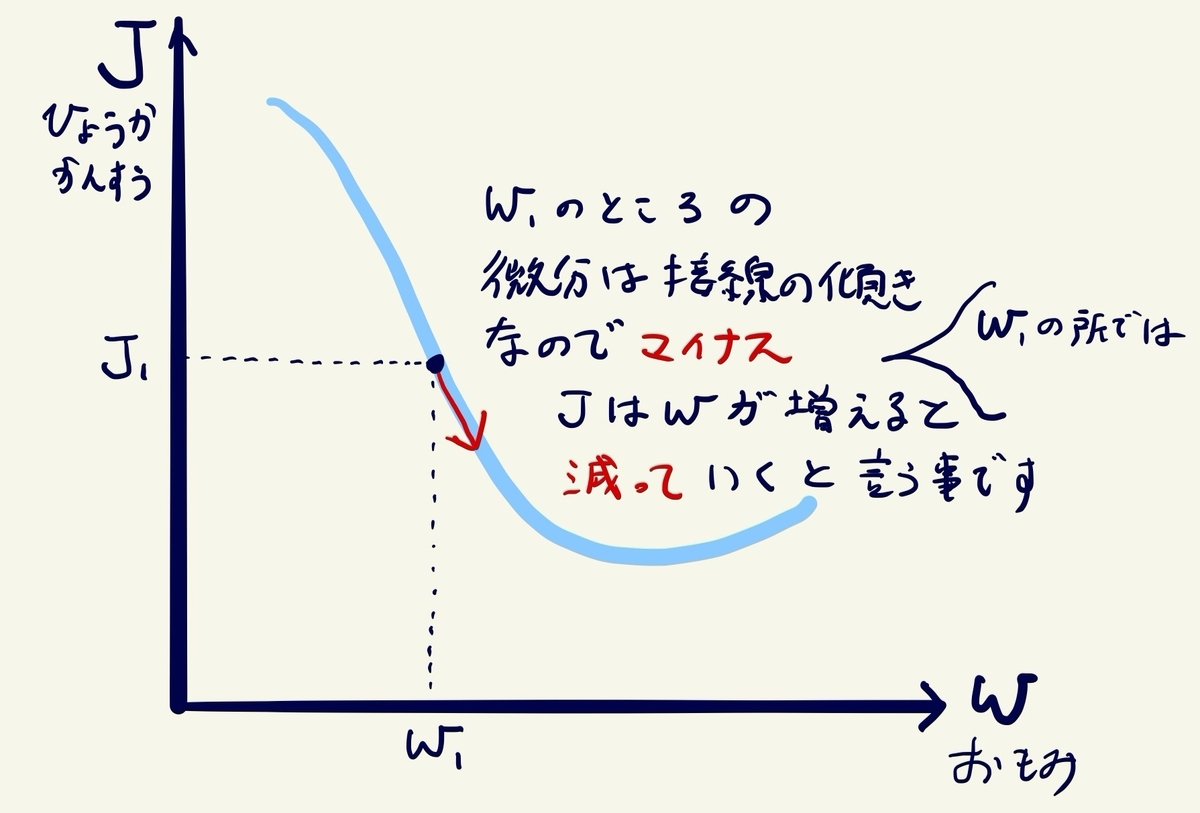
まず、今の重みの値のところの評価関数Jの微分値を求めます。その値がマイナスということは図の様にJの下り坂の 途中にいるので、重みをもう少し増やしてみるべきです。もし、微分値がプラスになったら、上りの坂道の 途中にいることになるので、いきすぎたので、重みは減らしたほうが良いです。
このように、少しづ重みを増やしたり、減らしたりして、坂道の一番底(最小値)に到るということです。
少しづつ増やす増やし方が大きすぎると行き過ぎたり、小さすぎると、到達するまでに何回もやることになり時間がかかります。 また、ぴったり底にいくのは難しいので、ある程度小さくなったら止めるというルールをもうけます。
このアルゴリズムは遅いのでさらに、誤差逆伝搬法というのがありますが、またの機会にしたいと思います。
この様にして、重みを決定することで、ニューラルネットワークは任意の関数を表現できる様になります。
おわりに
本当は、実際に計算した結果などを示したいと思って書き始めましたが そこまで行き着くのは簡単ではありませんでした。
本記事では以下のことをまとめてみました。
- ニューラルネットワークでできること
- ニューラルネットワークとはどうなってるのか
- 学習とはどんなことなのか
は説明できたのかなと思います。
今後、もう少し深く取り上げられたらと思っています。
巷には機械学習のツールがあふれ、それらの使い方がたくさん書かれていますが、 その中身を少しでも知る機会が増えればと思い 力不足ですが記事にしてみました。
参考文献
今回の記事を書くにあたり、次の本で再勉強しました。だいぶ前に買って積読(つんどく)状態でしたが 非常に良い本だとおもいます。ニューラルネットワーク や人工知能 の勉強に おすすめです。

